Question

Using integration, find the area of the region bounded by the ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$

Answer 1

Hint:Plot the curve on a graph. Observe that the curve is symmetrical in all the four quadrants. Hence find the area in the first quadrant, and hence the area of the ellipse will be four times the area in the first quadrant. For finding the area in the first curve quadrant express y in terms of x. Note that y>0 and hence take only the positive sign. Then use the fact that the area under the curve is given by $\int_{a}^{b}{ydx}$. Substitute suitable values of a and b and integrate and hence find the area.

Complete step-by-step answer:

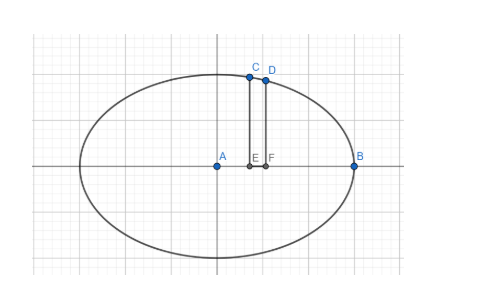
As is evident from the graph that the curve is symmetrical in the four quadrants. Hence, we will find the area in the first quadrant, and then the total area will be four times the area in the first quadrant.
Now, we have
$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
Subtracting $\dfrac{{{x}^{2}}}{{{a}^{2}}}$ from both sides, we get
$\dfrac{{{y}^{2}}}{{{b}^{2}}}=1-\dfrac{{{x}^{2}}}{{{a}^{2}}}$
Multiplying both sides by ${{b}^{2}}$, we get
${{y}^{2}}={{b}^{2}}\left( 1-\dfrac{{{x}^{2}}}{{{a}^{2}}} \right)$
Hence, we have
$y=\pm b\sqrt{1-\dfrac{{{x}^{2}}}{{{a}^{2}}}}=\pm \dfrac{b}{a}\sqrt{{{a}^{2}}-{{x}^{2}}}$
Now since in the first quadrant, y>0.
Hence, we have
$y=\dfrac{b}{a}\sqrt{{{a}^{2}}-{{x}^{2}}}$
Now consider the vertical strip CDEF.
Here CE = y and EF = dx
Hence the area of the strip will be ydx.
The area in the first quadrant will be the sum of the area of these vertical strips from A to B.
Now at point B, we have y = 0
Hence $\dfrac{{{x}^{2}}}{{{a}^{2}}}=1\Rightarrow {{x}^{2}}={{a}^{2}}\Rightarrow x=\pm a$
Since the abscissa of point B is positive, we have $x=a$.
Hence the area in the first quadrant will be $\int_{0}^{a}{ydx}$
Substituting the value of y, we get
The area in the first quadrant is $\int_{0}^{a}{\dfrac{b}{a}\sqrt{{{a}^{2}}-{{x}^{2}}}dx}$
Let $I=\int_{0}^{a}{\dfrac{b}{a}\sqrt{{{a}^{2}}-{{x}^{2}}}dx}$
Finding the value of I:
Put x = asint.
Differentiating both sides with respect to t, we get
$\dfrac{dx}{dt}=a\cos tdt\Rightarrow dx=a\cos tdt$
When x = 0, we have $a\sin t=0\Rightarrow \sin t=0\Rightarrow t=0$
When x = a, we have $a\sin t=a\Rightarrow \sin t=1\Rightarrow t=\dfrac{\pi }{2}$
Hence we have
$I=\dfrac{b}{a}\int_{0}^{\dfrac{\pi }{2}}{\sqrt{{{a}^{2}}-{{a}^{2}}{{\sin }^{2}}t}a\cos tdt}=ab\int_{0}^{\dfrac{\pi }{2}}{\sqrt{1-{{\sin }^{2}}t}\cos tdt}$
Now, we know that $1-{{\sin }^{2}}t={{\cos }^{2}}t$
Hence, we have
$I=ab\int_{0}^{\dfrac{\pi }{2}}{\sqrt{{{\cos }^{2}}t}\cos tdt}=ab\int_{0}^{\dfrac{\pi }{2}}{\left| \cos t \right|\cos tdt}$
Since in the interval $\left( 0,\dfrac{\pi }{2} \right)$ cost is positive, we have $\left| \cos t \right|=\cos t$
Hence, we have
$I=ab\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{2}}tdt}\text{ }\left( i \right)$
We know that $\int_{a}^{b}{f\left( x \right)dx}=\int_{a}^{b}{f\left( a+b-x \right)dx}$
Hence, we have
$I=ab\int_{0}^{\dfrac{\pi }{2}}{{{\cos }^{2}}\left( \dfrac{\pi }{2}-x \right)dx}$
We know that $\cos \left( \dfrac{\pi }{2}-x \right)=\sin x$
Hence, we have
$I=ab\int_{0}^{\dfrac{\pi }{2}}{{{\sin }^{2}}x}dx\text{ }\left( ii \right)$
Adding equation (i) and equation (ii), we get
$2I=ab\int_{0}^{\dfrac{\pi }{2}}{\left( {{\sin }^{2}}t+{{\cos }^{2}}t \right)dt}$
We know that ${{\sin }^{2}}t+{{\cos }^{2}}t=1$
Hence, we have
$2I=ab\int_{0}^{\dfrac{\pi }{2}}{1dt}=ab\left. t \right|_{0}^{\dfrac{\pi }{2}}=ab\left( \dfrac{\pi }{2}-0 \right)=\dfrac{\pi ab}{2}$
Dividing both sides by 2, we get
$I=\dfrac{\pi ab}{4}$
Hence the area in the first quadrant is $\dfrac{\pi ab}{4}$
Hence the total area of the ellipse is $4\times \dfrac{\pi ab}{4}=\pi ab$

Note: [1] We can directly solve I using the fact that $\int{\sqrt{{{a}^{2}}-{{x}^{2}}}=\dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{a}}$
Hence, we have
$\begin{align}
  & I=\dfrac{b}{a}\left( \left. \dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{a} \right|_{0}^{a} \right)=\dfrac{b}{a}\left[ \left( \dfrac{a}{2}\sqrt{{{a}^{2}}-{{a}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{a}{a} \right)-\left( \dfrac{0}{2}\sqrt{{{a}^{2}}-{{0}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{0}{a} \right) \right] \\
 & =\dfrac{b}{a}\left[ \left( 0+\dfrac{{{a}^{2}}}{2}\times \dfrac{\pi }{2} \right)-\left( 0-0 \right) \right]=\dfrac{\pi ab}{4} \\
\end{align}$
Which is the same as obtained above.