Question

Using disk or ring method, how do you find the volume of \[y = {x^2} - x,y = 3 - {x^2}\] about \[y = 4\] ?

Answer 1

Hint: Here, we find the volume of the given function using the disk methods. The disk method, also known as the method of disks or rings, is a way to calculate the volume of a solid of revolution by taking the sum of cross-sectional areas of infinitesimal thickness of the solid. The volume V of a solid of revolution, \[V = \pi \int\limits_a^b {{{\left( {{{\left( {f(x)} \right)}^2} - {{\left( {g(x)} \right)}^2}} \right)}^{}}dx} \] .

Complete step by step solution:
The given equation of parabola, we have
 \[
  y = {x^2} - x \to \left( 1 \right) \\
  y = 3 - {x^2} \to \left( 2 \right) \\
  y = 4 \to \left( 3 \right) \\
 \]
The region enclosed by the three curve in the below graph,

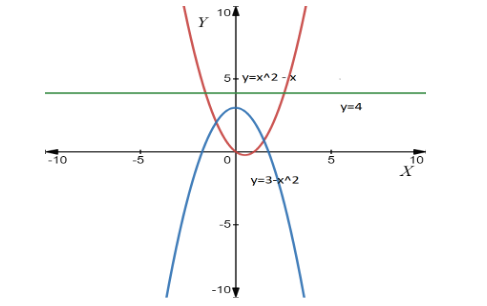
The volume V of a solid of revolution, \[V = \pi \int\limits_a^b {{{\left( {{{\left( {f(x)} \right)}^2} - {{\left( {g(x)} \right)}^2}} \right)}^{}}dx} \] .
Where, \[V - \] Volume of solid
 \[a - \] Least value of \[x\] of \[f(x)\]
 \[b - \] Highest value of \[x\] of \[f(x)\]
 \[f(x) - \] The value of radius of the disc
 \[dx - \] The value of height of the disc
 To find the point of intersection, where the two parabola meets,
 \[
  {x^2} - x = 3 - {x^2} \\
  {x^2} - x - 3 + {x^2} = 0 \;
 \]
By simplifying the equation to find the point of intersection
 \[
  2{x^2} - x - 3 = 0 \\
  x(2x - 1) = 3 \;
 \]
To simplify, we get
 \[x = 3\] ,
Then, another factor is
 \[
  2x - 1 = 3 \\
  2x = 3 + 1 \\
  x = \dfrac{4}{2} = 2 \;
 \]
The point of intersection, \[(a,b) = (2,3)\]
Let the given parabola equation,
 \[
  f(x) = {x^2} - x \\
  g(x) = 3 - {x^2} \;
 \]
To find the volume,
 \[V = \pi \int\limits_a^b {{{\left( {{{\left( {f(x)} \right)}^2} - {{\left( {g(x)} \right)}^2}} \right)}^{}}dx} \]
By substituting values in the formula
 \[
    \\
  V = \pi \int\limits_2^3 {\left( {\left( {{{({x^2})}^2} - 2{x^2} \cdot x + {x^2}} \right) - \left( {{3^2} - 2 \times 3 \cdot {x^2} + {{\left( {{x^2}} \right)}^2}} \right)} \right)dx} \\
  V = \pi \int\limits_2^3 {\left( {\left( {{x^4} - 2{x^3} + {x^2}} \right) - \left( {9 - 6{x^2} + {x^4}} \right)} \right)dx} \;
 \]
To simply it by apply the algebraic formula, \[{(a - b)^2} = {a^2} - 2ab + {b^2}\]
 \[V = \pi \int\limits_2^3 {\left( {\left( {{{({x^2})}^2} - 2{x^2} \cdot x + {x^2}} \right) - \left( {{3^2} - 2 \times 3 \cdot {x^2} + {{\left( {{x^2}} \right)}^2}} \right)} \right)dx} \]
 \[V = \pi \int\limits_2^3 {\left( {\left( {{x^4} - 2{x^3} + {x^2}} \right) - \left( {9 - 6{x^2} + {x^4}} \right)} \right)dx} \]
To evaluate it by using integral, we get
 \[V = \pi \left[ {\left( {\dfrac{{{x^5}}}{5} - \dfrac{{2{x^4}}}{4} + \dfrac{{{x^3}}}{3}} \right) - \left( {9x - \dfrac{{6{x^3}}}{3} + \dfrac{{{x^5}}}{5}} \right)} \right] _2^3\]
By simplify the above equation, we get
 \[V = \pi \left[ {\dfrac{{{x^5}}}{5} - \dfrac{{2{x^4}}}{4} + \dfrac{{{x^3}}}{3} - 9x + \dfrac{{6{x^3}}}{3} - \dfrac{{{x^5}}}{5}} \right] _2^3\]
Performing addition and subtraction to simplify, we get
 \[V = \pi \left[ { - \dfrac{{2{x^4}}}{4} + \dfrac{{7{x^3}}}{3} - 9x} \right] _2^3\]
Solving the equation by substitute upper and lower limit, we get
 \[V = \pi \left[ {\left( { - \dfrac{{2 \times {3^4}}}{4} + \dfrac{{7 \times {3^3}}}{3} - 9 \times 3} \right) - \left( { - \dfrac{{2 \times {2^4}}}{4} + \dfrac{{7 \times {2^3}}}{3} - 9 \times 2} \right)} \right] \]
By simplify the power of the value,
 \[V = \pi \left( { - \dfrac{{2 \times 81}}{4} + \dfrac{{7 \times 27}}{3} - 9 \times 3 + \dfrac{{2 \times 16}}{4} - \dfrac{{7 \times 8}}{3} + 9 \times 2} \right)\]
By performing operation for the same denominator value, we get
 \[V = \pi \left( {\dfrac{{ - (2 \times 81) + (2 \times 16)}}{4} + \dfrac{{(7 \times 27) - (7 \times 8)}}{3} + 9( - 3 + 2)} \right)\]
 \[V = \pi \left( {\dfrac{{2( - 81 + 16)}}{4} + \dfrac{{7(27 - 8)}}{3} + 9( - 1)} \right)\]
Now, we get
 \[V = \pi \left( {\dfrac{{2( - 65)}}{4} + \dfrac{{7(19)}}{3} - 9} \right)\]
Take LCM on above equation, we get
 \[V = \pi \left( {\dfrac{{2( - 65)(3) + 7(19)(4) - 9(12)}}{{12}}} \right) = \pi \left( {\dfrac{{ - 390 + 532 - 108}}{{12}}} \right)\]
 \[V = \pi \dfrac{{(532 - 498)}}{{12}} = \pi \dfrac{{34}}{{12}} = \pi \dfrac{{17}}{6}\]
 \[V = \dfrac{{17}}{6}\pi \]
Therefore, the volume bounded by the region, \[V = \dfrac{{17}}{6}\pi \]
So, the correct answer is “ \[V = \dfrac{{17}}{6}\pi \] ”.

Note: A solid of revolution is formed by rotating a two-dimensional function around an axis to produce a three-dimensional shape (either a full solid or a ring).Here we use integration to solve the volume bounded by the region with the point of intersection. We remember the formula for volume met by the two parabola functions.