Question

How do you use the graphing utility to graph $f(x) = - 2{x^2} + 10x$ and identify the $x$ intercepts and the vertex?

Answer 1

Hint: This problem deals with the conic sections. A conic section is a curve obtained as the intersection of the surface of a cone with a plane. There are three such types of conic sections which are, the parabola, the hyperbola and the ellipse. This problem is regarding one of those conic sections, which is a parabola. The general form of an equation of a parabola is given by ${x^2} = - 4ay$.

Complete step-by-step solution:
Here consider the given parabola of equation $f(x) = - 2{x^2} + 10x$
Here let the function $f(x)$ be $y$, as given below:
$ \Rightarrow y = f(x)$
So the equation of the parabola is given by:
$ \Rightarrow y = - 2{x^2} + 10x$
Taking the term $2x$ common on the right hand side of the above equation as given below:
$ \Rightarrow y = - 2x\left( {x - 5} \right)$
To find the $x$ intercepts, put $y = 0$, as given below:
$ \Rightarrow - 2x\left( {x - 5} \right) = 0$
$\therefore x = 0;x = 5$
So the $x$ intercepts are 0 and 5.
The graph of the given parabola is shown below:

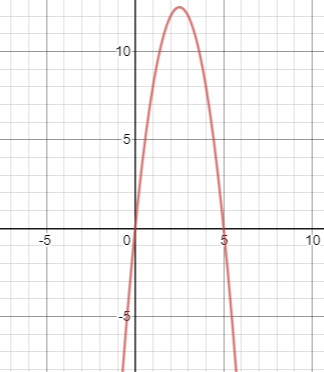
Now consider the given parabola equation $y = - 2{x^2} + 10x$, writing this in its standard form as shown below:
$ \Rightarrow {\left( {x - 2.5} \right)^2} = - 12\left( {y - 12.5} \right)$
If the above equation is simplified, the given equation of parabola $y = - 2{x^2} + 10x$, will be obtained.
Here in the above equation, it shows that the vertex $V$ is :
$ \Rightarrow V = \left( {2.5,12.5} \right)$
This parabola has its axis parallel to y-axis.

The $x$ intercepts are 0 and 5, whereas the vertex is $\left( {2.5,12.5} \right)$.

Note: Please note that if the given parabola is ${x^2} = - 4ay$, then the vertex of this parabola is the origin $\left( {0,0} \right)$, and there is no intercept for this parabola as there are no terms of x or y. If the equation of the parabola includes any terms of linear x or y, then the vertex of the parabola is not the origin, the vertex has to be found by simplifying it into its particular standard form.