Question

How can you use proportion and similar triangles to indirectly measure large objects, such as height of building and mountains?

Answer 1

Hint: Now to find the height of the building we will first consider the triangle cast by the building and the shadow of the building. Now consider another object whose height is measurable. Now consider the triangle caused by the object and its shadow. Now these two triangles are similar. Hence we will take the ratio of the sides and find the height of the building by measuring the shadow of the building, second object and height of object.

Complete step by step solution:
Now we know that if the triangles are similar then the corresponding sides are in the same ratio.
Hence if we have $\Delta ABC\sim \Delta PQR$ then we can say that $\dfrac{AB}{PQ}=\dfrac{BC}{QR}=\dfrac{AC}{PR}$
Now let us say we want to measure the height of a building BD.
Let BD’ be the shadow of a building.
Hence we can say that we have a triangle $\Delta DBD'$ .
Now let us say let us say we have another pole or object making the same angle with the ground. Note that the length of this pole must be measurable.
Now let this pole be PQ and the shadow of the pole be PQ’
Hence again we have the triangle $\Delta PQP'$
Now since the pole and the building are in the same surrounding the triangles made by the shadows will be similar.

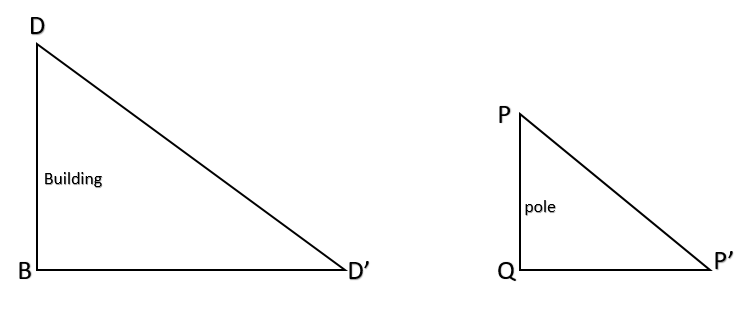
Now we know can measure BD’, PQ and PQ’
Now since we have $\Delta BDB'\cong \Delta QPQ'$ we can say
$\Rightarrow \dfrac{BD}{BD'}=\dfrac{QP}{QP'}$
Now we know the values BD’, PQ and PQ’ hence we can easily find the value of BD.
Hence we can find the height of the building.

Note: Now note that here we have the triangles are similar and not congruent. The meaning of similar is that the triangles are in the same ration. The meaning of congruent is that the triangles are equal and of the same dimensions. Hence not to be confused between two.