Question

Use number line and add the following integers:
\[\left( { - 2} \right) + 8 + \left( { - 4} \right)\]

Answer 1

Hint: The question is to use the number line and add the given integers. Integers are whole numbers with positive or negative sign which means numbers with positive sign are positive integers and numbers with negative sign are negative integers. So, the range of integers is from negative infinity to positive infinity. In this question, we will add the given integers.

Complete answer:
The question is to add the integers \[\left( { - 2} \right) + 8 + \left( { - 4} \right)\] using a number line.
Number line is a straight line which extends up to infinity in the positive as well as negative side. Firstly, we will plot number line, then we will locate the integers \[\left( { - 2} \right),8\] and \[\left( { - 4} \right)\] on the number line, and at last, we will add them using number line.
Plotting on the number line:

This is the number line and we had plotted the integers \[\left( { - 4} \right)\] to \[8\] on it.
In the next step, we will locate \[\left( { - 2} \right),8\] and \[\left( { - 4} \right)\] on it and we will get

We have to add these three plotted integers on the number line. To do that, we have to make the difference between \[\left( { - 2} \right)\] and \[2\] in such a way that when we move from \[0\] to \[\left( { - 2} \right)\], we get \[\left( { - 2} \right)\] and when we move from \[0\] to \[\left( 2 \right)\], we get \[2\]. It means the addition of \[\left( { - 2} \right)\] and \[\left( 2 \right)\] results in zero \[\left( 0 \right)\].
In the same way, the result of addition of \[\left( { - 4} \right)\] and \[\left( 4 \right)\] results in zero \[\left( 0 \right)\].

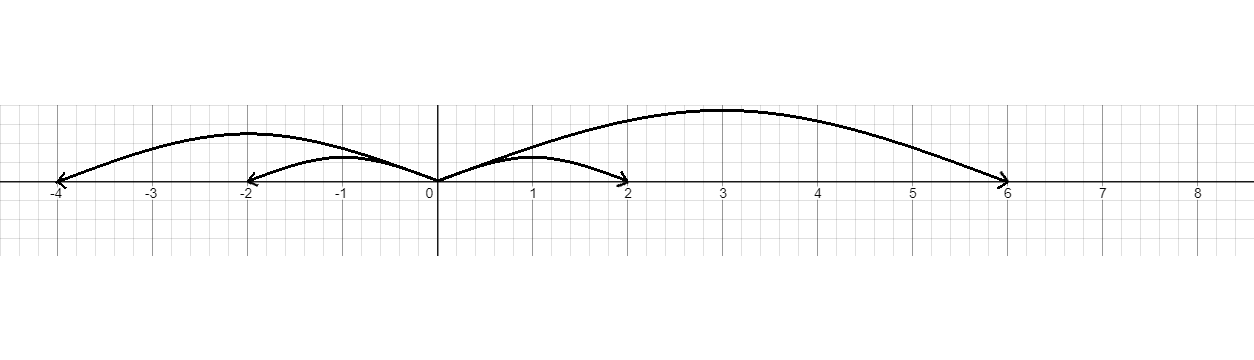
In addition to \[\left( { - 2} \right)\] and \[\left( 2 \right)\], the result is zero. On addition of \[\left( { - 4} \right)\] and \[\left( 6 \right)\] (from \[2\] to \[6\]), the result is zero and we are left with \[2\] (from \[6\] to \[8\]).
Therefore, using the number line, when we add the integers \[\left( { - 2} \right),8\] and \[\left( { - 4} \right)\], we get \[2\] as an answer. We have done it with a number line by plotting the numbers on it and then adding them by cancelling them with opposite signs.

Note: Zero \[\left( 0 \right)\] is also an integer. This is because zero is a whole number and all the whole numbers are integers. Fractional numbers or rational numbers are not integers because they are not whole numbers. Also, decimals are not integers because they are not whole numbers. All whole numbers are integers but all integers are not whole numbers.