Question

How do I use DeMoivre's theorem to find out \[{{\left( -3+3i \right)}^{3}}\]?

Answer 1

Hint: To solve this complex expression, first assume \[z=-3+3i\] and then change this complex number into trigonometric form that is \[z=\rho \left[ \cos \left( \theta \right)+i\sin \left( \theta \right) \right]\] and then apply DeMoivre’s theorem which is \[{{z}^{n}}={{\rho }^{n}}\left[ \cos \left( n\theta \right)+i\sin \left( n\theta \right) \right]\] to get the value of \[{{z}^{3}}={{\left( -3+3i \right)}^{3}}\].

Complete step by step solution:
Let us suppose given complex number to be as follows:
\[z=-3+3i\]
\[\Rightarrow {{z}^{3}}={{\left( -3+3i \right)}^{3}}\]
To change this complex number into trigonometric form that is
\[z=\rho \left[ \cos \left( \theta \right)+i\sin \left( \theta \right) \right]...\left( 1 \right)\]
we need to find the value of \[\theta \] and \[\rho \] . We know that \[\rho =\sqrt{{{\left( x \right)}^{2}}+{{\left( y \right)}^{2}}}\]here \[x=-3\] and \[y=3\]. After applying these values, we get:
\[\Rightarrow \rho =\sqrt{{{\left( -3 \right)}^{2}}+{{\left( 3 \right)}^{2}}}\]
\[\Rightarrow \rho =\sqrt{9+9}\]
\[\Rightarrow \rho =3\sqrt{2}\]
To find the value of \[\theta \] formula is \[\theta =\arctan \left( \dfrac{y}{x} \right)\] here \[x=-3\] and \[y=3\]. After applying these values, we get:
\[\Rightarrow \theta =\arctan \left( \dfrac{3}{-3} \right)\]
\[\Rightarrow \theta =\arctan \left( -1 \right)\]
\[\Rightarrow \theta =\dfrac{3\pi }{4}\]
Now substitute the value of \[\theta \] and \[\rho \] in equation \[\left( 1 \right)\] to convert in trigonometry form we get:
\[\Rightarrow z=3\sqrt{2}\left[ \cos \left( \dfrac{3\pi }{4} \right)+i\sin \left( \dfrac{3\pi }{4} \right) \right]\]
And apply DeMoivre’s theorem which is \[{{z}^{n}}={{\rho }^{n}}\left[ \cos \left( n\theta \right)+i\sin \left( n\theta \right) \right]\] in equation \[{{z}^{3}}={{\left( -3+3i \right)}^{3}}\] we get:
\[\Rightarrow {{z}^{3}}={{\left( 3\sqrt{2} \right)}^{3}}\left[ \cos \left( 3\cdot \dfrac{3\pi }{4} \right)+i\sin \left( 3\cdot \dfrac{3\pi }{4} \right) \right]\]
\[\Rightarrow {{z}^{3}}={{\left( 3\sqrt{2} \right)}^{3}}\left[ \cos \left( \dfrac{9\pi }{4} \right)+i\sin \left( \dfrac{9\pi }{4} \right) \right]\]
\[\Rightarrow {{z}^{3}}=54\sqrt{2}\left[ \cos \left( \dfrac{9\pi }{4} \right)+i\sin \left( \dfrac{9\pi }{4} \right) \right]\]
We can further split this angle as \[\dfrac{9\pi }{4}=2\pi +\dfrac{\pi }{4}\] and replace it in the above equation we get:
\[\Rightarrow {{z}^{3}}=54\sqrt{2}\left[ \cos \left( 2\pi +\dfrac{\pi }{4} \right)+i\sin \left( 2\pi +\dfrac{\pi }{4} \right) \right]\]
According to the one of the trigonometric properties of cosine and sine one of them is \[\cos \left( 2\pi +\theta \right)=\cos \left( \theta \right)\] and \[\sin \left( 2\pi +\theta \right)=\sin \left( \theta \right)\] using these in the above equation we get:
\[\Rightarrow {{z}^{3}}=54\sqrt{2}\left[ \cos \left( \dfrac{\pi }{4} \right)+i\sin \left( \dfrac{\pi }{4} \right) \right]\]
We know that value of \[\cos \left( \dfrac{\pi }{4} \right)=\sin \left( \dfrac{\pi }{4} \right)=\dfrac{1}{\sqrt{2}}\], by substituting this value we get:
\[\Rightarrow {{z}^{3}}=54\sqrt{2}\left[ \dfrac{1}{\sqrt{2}}+i\dfrac{1}{\sqrt{2}} \right]\]
Now we take LCM within the brackets and simplify we get:
\[\Rightarrow {{z}^{3}}=54\sqrt{2}\left[ \dfrac{1+i}{\sqrt{2}} \right]\]
As we can see \[\sqrt{2}\] is there in both numerator and denominators. So, it gets cancelled. Hence, we are left with the following:
\[\Rightarrow {{z}^{3}}=54\left[ 1+i \right]\]
After solving the bracket, we get:
\[\Rightarrow {{z}^{3}}=54+54i\]
Therefore, value of \[{{z}^{3}}={{\left( -3+3i \right)}^{3}}\] is \[{{z}^{3}}=54+54i\].

Note:
Students can go wrong by using wrong DeMoivre’s formula that is some students use \[{{z}^{n}}={{\rho }^{n}}\left[ n\cos \left( \theta \right)+n\sin \left( \theta \right)i \right]\] instead of \[{{z}^{n}}={{\rho }^{n}}\left[ \cos \left( n\theta \right)+i\sin \left( n\theta \right) \right]\] which further leads to the wrong result. Hence, it’s important to remember DeMoivre’s theorem which is \[{{z}^{n}}={{\rho }^{n}}\left[ \cos \left( n\theta \right)+i\sin \left( n\theta \right) \right]\] right. Also, you can find the value of \[\theta \] by observing the graph of given complex no. that is:

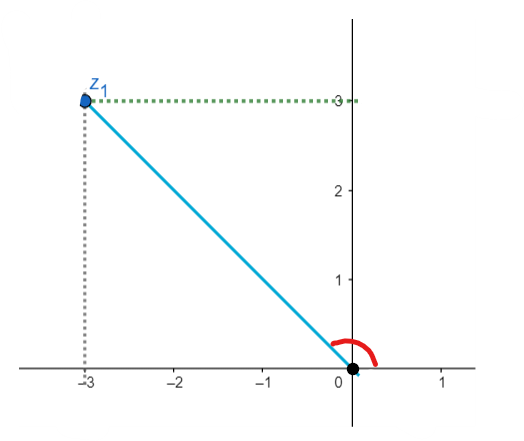
Clearly you can see the angle is equal to \[\dfrac{\pi }{2}+\dfrac{\pi }{4}=\dfrac{3\pi }{4}\]. Which implies \[\theta =\dfrac{3\pi }{4}\]