Question

How do you use a graphing calculator to find the limit of the sequence \[{a_n} = {\left( {\dfrac{1}{2}} \right)^n}\] ?

Answer 1

Hint: Here the given question based on geometric series. We have to plot a graph of the given function of the series. Firstly, we have to make a sequence of series by giving a n values, where n belongs to integers i.e., \[n \in I\] . After that plot a graph by taking n values in x-axis and \[{a_n}\] values in y-axis.

Complete step by step solution:
A geometric series is also termed as the geometric progression. It is a series formed by multiplying the first term by a fixed value to get the second term. This process is continued until we get a required number of terms in the series. Such a progression increases in a specific way and hence giving a geometric progression.
Consider, the given limit of the sequence:
 \[ \Rightarrow {a_n} = {\left( {\dfrac{1}{2}} \right)^n}\] where \[n \in I\] .
Now giving the n values … -3, -2, -1, 0, 1, 2, 3, … to the above equation simultaneously we get the values of \[{a_n}\] .
Now put \[n = - 3\] , then
 \[ \Rightarrow {a_{ - 3}} = {\left( {\dfrac{1}{2}} \right)^{ - 3}}\]
 \[ \Rightarrow {a_{ - 3}} = \dfrac{1}{{{2^{ - 3}}}}\]
 \[ \Rightarrow {a_{ - 3}} = {2^3} = 8\]
Put \[n = - 2\] , then
 \[ \Rightarrow {a_{ - 2}} = {\left( {\dfrac{1}{2}} \right)^{ - 2}}\]
 \[ \Rightarrow {a_{ - 2}} = {2^2} = 4\]
Put \[n = - 1\] , then
 \[ \Rightarrow {a_{ - 1}} = {\left( {\dfrac{1}{2}} \right)^{ - 1}}\]
 \[ \Rightarrow {a_{ - 1}} = {2^1} = 2\]
Put \[n = 0\] , then
 \[ \Rightarrow {a_0} = {\left( {\dfrac{1}{2}} \right)^0}\]
 \[ \Rightarrow {a_0} = 1\]
Put \[n = 1\] , then
 \[ \Rightarrow {a_1} = {\left( {\dfrac{1}{2}} \right)^1}\]
 \[ \Rightarrow {a_1} = 0.5\]
Put \[n = 2\] , then
 \[ \Rightarrow {a_2} = {\left( {\dfrac{1}{2}} \right)^2}\]
 \[ \Rightarrow {a_2} = \dfrac{1}{{{2^2}}} = \dfrac{1}{4}\]
 \[ \Rightarrow {a_2} = 0.25\]
Put \[n = 3\] , then
 \[ \Rightarrow {a_3} = {\left( {\dfrac{1}{2}} \right)^3}\]
 \[ \Rightarrow {a_3} = \dfrac{1}{{{2^3}}} = \dfrac{1}{8}\]
 \[ \Rightarrow {a_3} = 0.125\]
And so on…
Hence the sequence \[{a_n}\] as written as:
 \[ \Rightarrow {a_n} = \cdot \cdot \cdot ,8,4,2,1,0.5,0.25,0.125, \cdot \cdot \cdot \]
Now, we can plot the graph of \[{a_n} = {\left( {\dfrac{1}{2}} \right)^n}\] , by taking n values in x-axis and \[{a_n}\] values in y-axis.

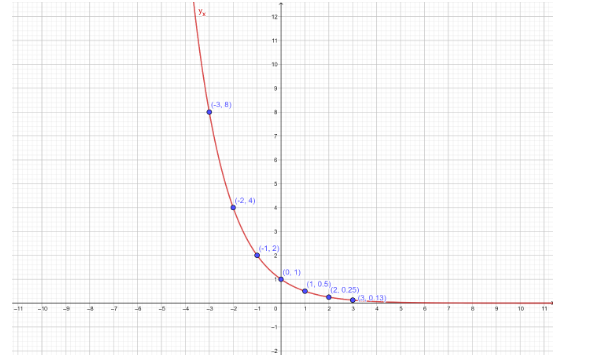
Note: The question is belonging to the concept of graph. To plot a graph first we have to choose which one is x-axis and y-axis. Or by choosing the value of x we can determine the value of y and then plotting the graphs for these points we obtain the result.