Question

Two-point charges ${{Q}_{1}}=400\mu C$ and ${{Q}_{2}}=100\mu C$ are kept fixed, 60cm apart in vacuum. Find intensity of the electric field at the midpoint of the line joining ${{Q}_{1}}\text{ and }{{\text{Q}}_{2}}$.

Answer 1

Hint: The space surrounding an electric charge, in which any other charge experiences a force is called electric field of charge. Use the formula of electric field intensity due to a point charge for point midpoint O due to A and B. Take resultant of both calculated electric fields. Take care of the resultant electric field. Value of k is one in vacuum.

Complete step by step solution:

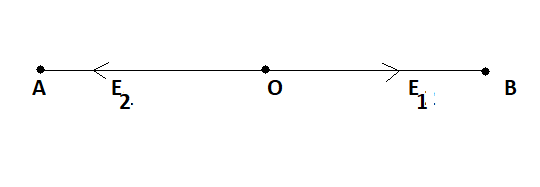
We have two charges ${{Q}_{1}}\text{ and }{{\text{Q}}_{2}}$ at A and B respectively, separated by a distance 60cm which is fixed. Now we need to find out the electric field at O which is a midpoint as given in the figure.
If O is midpoint then distance between AO and OB must be half of 60 which is 30cm.
We know that electric field is given by,
$E=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\times \dfrac{Q}{{{r}^{2}}}$
Where
Q= charge because of which electric field on midpoint O is affecting.
$E$= electric field where we want to calculate
r= distance between charge and point where we want to calculate the electric field.
Electric field at midpoint O because of A along the direction of AO is given by,
${{E}_{1}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\times \dfrac{{{Q}_{1}}}{{{r}^{2}}}$
(Since value of k=1 in vacuum)
Put the value in above equation from given data, we get
${{E}_{1}}=9\times {{10}^{9}}\times \dfrac{400\times {{10}^{-6}}}{{{(30\times {{10}^{-2}})}^{2}}}=\dfrac{9\times {{10}^{9}}}{{{(30\times {{10}^{-2}})}^{2}}}(400\times {{10}^{-6}})$
Electric field at midpoint O because of B along the direction of BO is given by,
${{E}_{2}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\times \dfrac{{{Q}_{2}}}{{{r}^{2}}}$
Put the value in above equation from given data, we get
${{E}_{2}}=9\times {{10}^{9}}\times \dfrac{100\times {{10}^{-6}}}{{{(30\times {{10}^{-2}})}^{2}}}=\dfrac{9\times {{10}^{9}}}{{{(30\times {{10}^{-2}})}^{2}}}(100\times {{10}^{-6}})$
Let’s say O is the origin then AO must be in a positive direction. And BO must be in a negative direction. So the resultant electric field is given by,
$\vec{E}={{\vec{E}}_{1}}-{{\vec{E}}_{2}}$
$\vec{E}=\dfrac{9\times {{10}^{9}}}{{{(30\times {{10}^{-2}})}^{2}}}(400-100)\times {{10}^{-6}}=\dfrac{9\times {{10}^{9}}\times {{10}^{-6}}\times 300}{{{(30\times {{10}^{-2}})}^{2}}}=3\times {{10}^{7}}N/C$
Hence intensity of the electric field at midpoint of the line joining${{Q}_{1}}\text{ and }{{\text{Q}}_{2}}$ is $3\times {{10}^{7}}N/C$


Note: Students should understand the direction of the electric field because it plays an important role while finding resultant electric fields. We know that direction of electric field lines always originate from charge and directed away from it if the charge is positive. If charge is negative, the electric field line will terminate at negative charge in this case charge is positive therefore direction of electric fields are away from it.