Question

Two-point charges $Q_1=2\mu C$ and $Q_2=1\mu C$ are placed as shown. The coordinates of the point P are (2cm,1cm). The electric intensity at P subtends an angle $\theta$ with the positive X axis. The value of $\theta$ is given by:
$A.\tan\theta=1$
$B. \tan\theta=2$
$C.\tan\theta=3$
$D. \tan\theta=4$

Answer 1

Hint: The electric field at a point due to a point charge separated at a particular distance. Then, after calculating the fields for two different charges, we can find the direction of the resultant electric field. So, the value of $\theta$ can be found.
Formula used: $E=\dfrac{1}{4\pi \epsilon_0}.\dfrac{q}{r^2}$

Complete step by step solution:
The electric field due to charge q at a distance of r is given by,
$E=\dfrac{1}{4\pi \epsilon_0}.\dfrac{q}{r^2}$
Now, we will find the electric field for the charge $Q_1$ and then the field for the charge $Q_2$. The first field will be denoted by $E_1$ whereas the second one will be denoted by $E_2$. Now, if $\theta$ be the angle as shown in the picture, then the value of $\tan\theta$ is given by $\dfrac{E_2}{E_1}$ .
The point P has the coordinates (2cm, 1cm). So, it is at a distance of 2 cm from $Q_1$ and at a distance of 1 cm from the charge $Q_2$.

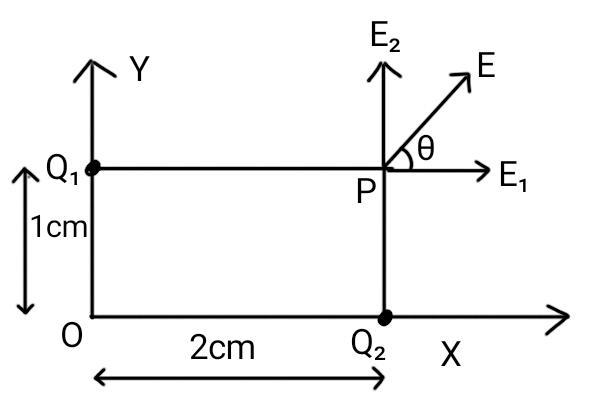
For the first field, we can see that the charge is $Q_1=2\mu C$. And the distance from charge $Q_1$ is 2 cm. So, the electric field is given by,
$E=\dfrac{1}{4\pi \epsilon_0}.\dfrac{Q_1}{2^2}=\dfrac{1}{4\pi \epsilon_0}.\dfrac{2}{4}$
Similarly, for the second field, the charge is $Q_2=1 \mu C$. And the corresponding distance is 1cm. So, the field is,
$E=\dfrac{1}{4\pi \epsilon_0}.\dfrac{1}{1^2}$
After making $\dfrac{E_2}{E_1}$ we find that,
$\tan \theta =\dfrac{{{E}_{2}}}{{{E}_{1}}}=2$
So, option B is the correct answer.

Additional information:
The electric field intensity is defined as the force felt by a unit positive charge placed at the point of interest. It is actually the number of lines of force per unit area. The unit of the electric field is volt per meter. In the used formula, $\epsilon_0$ is called the permittivity of free space.

Note: If the angle were not with x axis but with the y axis, then the value of $\tan \theta $ would be $\dfrac{E_1}{E_2}$. Put the correct charge with the corresponding distance in the formula. While taking the ratio of two same quantities, make sure to keep them in the same unit.