Question

Two wires of resistance $ {R_1} $ and $ {R_2} $ at $ {0^0}C $ have temperature coefficient of resistance $ {\alpha _1} $ and $ {\alpha _2} $ , respectively. These are joined in series. The effective temperature coefficient of resistance is:
(A) $ \dfrac{{{\alpha _1} + {\alpha _2}}}{2} $
(B) $ \sqrt {{\alpha _1}{\alpha _2}} $
(C) $ \dfrac{{{\alpha _1}{R_1} + {\alpha _2}{R_2}}}{{{R_1} + {R_2}}} $
(D) $ \dfrac{{\sqrt {{R_1}{R_2}{\alpha _1}{\alpha _2}} }}{{\sqrt {R_1^2 + R_2^2} }} $

Answer 1

Hint: Here, we have the two wires with resistances and their coefficients of resistance at $ {0^0}C $ and effective temperature coefficient is asked. So, here we have to use the concept of resistances in series and increase the temperature of each resistance by $ t $ .

Complete answer:
Here, we have two resistances and we have to increase their temperature by $ t $ , $ {\alpha _1} $ and $ {\alpha _2} $ are the temperature coefficients of $ {R_1} $ and $ {R_2} $ , respectively. Let us show it by the diagram below:

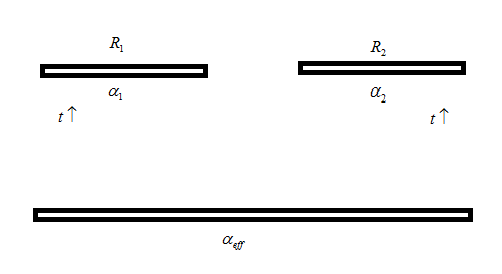
Those resistances are given by,
 $ \begin{gathered}
  R{t_1} = {R_1}(1 + {\alpha _1}t) \\
  R{t_2} = {R_2}(1 + {\alpha _2}t) \\
\end{gathered} $ (since, temperature is increased by $ t $ )
If these resistances are joined in series then the resistances equivalent is given by
 $ {R_{eq}} = R{t_1} + R{t_2} $
 $ \Rightarrow {R_{eq}} = {R_1}(1 + {\alpha _1}t) + {R_2}(1 + {\alpha _2}t) $ …..(putting all the values from above)
 $ = {R_1} + {R_1}{\alpha _1}t + {R_2} + {R_2}{\alpha _2}t $
 $ = ({R_1} + {R_2}) + t({R_1}{\alpha _1} + {R_2}{\alpha _2}) $
 $ = ({R_1} + {R_2})\left( {1 + \dfrac{{{R_1}{\alpha _1} + {R_2}{\alpha _2}}}{{({R_1} + {R_2})}}t} \right) $
Now, comparing this equation with $ {R_{eq}} = R(1 + {\alpha _{eff}}t) $
We observe here that
 $ R = ({R_1} + {R_2}) $ and $ {\alpha _{eff}} = \dfrac{{{R_1}{\alpha _1} + {R_2}{\alpha _2}}}{{({R_1} + {R_2})}} $
Here, we obtained the effective temperature coefficient as $ {\alpha _{eff}} = \dfrac{{{R_1}{\alpha _1} + {R_2}{\alpha _2}}}{{({R_1} + {R_2})}} $
Thus the correct option is C.

Note:
Here, the wires with different resistances are joined in series and their temperature is increased. Effective temperature coefficient is the resistance-change factor per degree Celsius of temperature.
Both wires have temperature coefficient and hence we obtained the effective temperature coefficient by the above mentioned procedure in the answer.