Question

Two wires carrying
A. Parallel current repels each other.
B. Anti-parallel current attracts each other.
C. Antiparallel current repels each other.
D. Equal magnitudes of Anti parallel current attract each other.

Answer 1

Hint: Analyse how the wires influence one another. Use the theory that a long straight wire, which is carrying some current produces magnetic field lines in the surroundings in the form of concentric circles. When a straight current carrying conductor is placed in an external magnetic field, the conductor experiences a magnetic force given by, $\overrightarrow{F}=i\left( \overrightarrow{l}\times \overrightarrow{B} \right)$. The direction of this force is given by Fleming’s left hand rule.

Complete answer:
We must know that Fleming’s left hand rule gives the direction of force acting on a current carrying conductor. Here, the forefinger represents the direction of the field, the second finger represents that of current, and the thumb gives the direction of force.
 

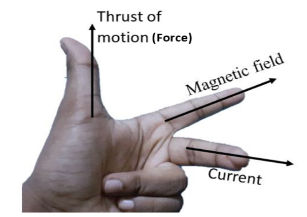
Now, let us consider two infinitely long straight wires. Let the two wires be placed free and parallel to each other. The two wires carry currents ${{i}_{1}}$ and ${{i}_{2}}$.

Case 1: Parallel current (current in both wires in same direction)
In this case, the directions of both currents are the same. Let the perpendicular distance between them be d.

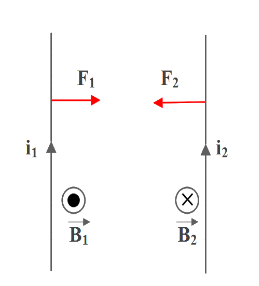
Applying Fleming’s left hand rule and finding the direction of force, we can find that they are acting as two forces attracting towards each other.
So, we can conclude that parallel currents attract each other.

Case 2: Anti-parallel current (current in both wires in opposite direction)
In this case, the directions of both currents are opposite. Let the perpendicular distance between them be d.

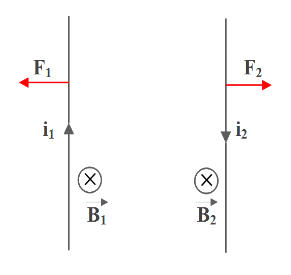
Applying Fleming’s left hand rule and finding the direction of force, we can find that they are acting as two forces repelling each other.
So, we can conclude that anti-parallel currents repel each other.

So, the correct answer is “Option C”.

Note:
Keep in mind that two straight current carrying wires parallel to each other will not always repel each other. It depends on the direction of currents in both wires. Also the magnitude of this force is given by,
$\overrightarrow{F}=i\left( \overrightarrow{l}\times \overrightarrow{B} \right)=\dfrac{{{\mu }_{0}}{{I}_{1}}{{I}_{2}}}{2\pi d}L$
Where,
${{\mu }_{0}}$ is the permeability of vacuum.
${{I}_{1}}$ and ${{I}_{2}}$ are current flowing through each wire.
$L$ is the length of the wire.
And $d$ is the distance between two wires.