Question

Two stars are \[10\] light years away from the earth. They are seen through a telescope of objective diameter \[30\,{\text{cm}}\] . The wavelength of light is \[600\,{\text{nm}}\] . To see the stars just resolved by the telescope, the minimum distance between them should be ( \[1\] light year equals \[9.46 \times {10^{15}}\,{\text{m}}\] ) of the order of:
A. \[{10^8}\,{\text{km}}\]
B. \[{10^{10}}\,{\text{km}}\]
C. \[{10^{11}}\,{\text{km}}\]
D. \[{10^6}\,{\text{km}}\]

Answer 1

Hint:First of all, we will draw the schematic diagram of the scenario. After that we will apply the formula of the resolution of the telescope. We will replace the angular separation by distance between the stars and distance from the earth in a correct way. We will substitute the required values and obtain the answer.

Formula used:
The resolution of a telescope can be related with the formula as given below:
\[\theta = \dfrac{{1.22 \times \lambda }}{D}\] …… (1)
Where,
\[\theta \] indicates the angular separation.
\[\lambda \] indicates the wavelength of the light.
\[D\] indicates the diameter of the objective lens.

Complete step by step answer:
In the given question, we are supplied with the following data:
There are two stars which are at a distance of \[10\] light years away from the earth.They are seen through a telescope whose objective is of diameter \[30\,{\text{cm}}\] .We are asked to find the minimum distance between the two stars so that they are just resolved by the telescope.We are also given that \[1\] light year equals \[9.46 \times {10^{15}}\,{\text{m}}\] .

To begin with, we need to draw a simple diagram to depict the scenario, for better understanding.

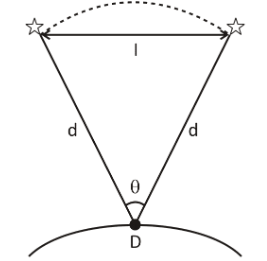
In the given diagram, the angular separation of the two stars as viewed from the earth, through the telescope, is \[\theta \] .
From the diagram the angular separation can be written as given below:
\[\theta = \dfrac{l}{d}\]

Now, we use the equation (1) and we get:
$\theta = \dfrac{{1.22 \times \lambda }}{D} \\
\Rightarrow \dfrac{l}{d} = \dfrac{{1.22 \times \lambda }}{D} \\
\Rightarrow l = \dfrac{{1.22 \times \lambda \times d}}{D} \\
\Rightarrow l = \dfrac{{1.22 \times 600 \times {{10}^{ - 9}} \times 10 \times 9.46 \times {{10}^{15}}}}{{30 \times {{10}^{ - 2}}}} \\
\Rightarrow l = 2.3 \times {10^{11}}\,{\text{m}} \\
\Rightarrow l = 2.3 \times {10^{11}} \times {10^{ - 3}}\,{\text{km}} \\
\Rightarrow l = 2.3 \times {10^8}\,{\text{km}}$
Therefore, the distance between the two stars is found to be \[2.3 \times {10^8}\,{\text{km}}\] .
Hence, the order is \[{10^8}\,{\text{km}}\] .

The correct option is A.

Note:While solving the problem, it is important to draw the diagram, as it reduces most of the chances to get wrong. As the two stars are present at a very large distance, we can assume the distance of separation to be arc. Most of the students get confused at this point. Larger the diameter of the objective is, higher is the resolution of the telescope.