Question

Two similar coils of radius $R$are lying concentrically with their planes at right angles to each other. The currents flowing in them are $I$and $2I$respectively. The resultant magnetic field induction at the centre will be
A) $\dfrac{{{\mu }_{0}}I}{2R}$
B) $\dfrac{{{\mu }_{0}}I}{R}$
C) $\dfrac{\sqrt{5}{{\mu }_{0}}I}{2R}$
D) $\dfrac{3{{\mu }_{0}}I}{2R}$

Answer 1

Hint: Concentric circles have a common centre. Similarly, concentric coils have a common centre. Magnetic field induction refers to the production of electromotive force across a current carrying conductor in a changing magnetic field.

Complete step by step answer:
When current is passed through a coil, a magnetic field is created in the coil. This magnetic field restricts the current to flow through the coil. Here, in this question, two coils of the same radius $R$ are used. It is said that both the coils are concentric, but the planes of the coils are at right angles. This suggests that both the coils have a common centre, but the planes of the coils are perpendicular to each other. We are supposed to find the magnetic field induction at the common centre of both the coils.

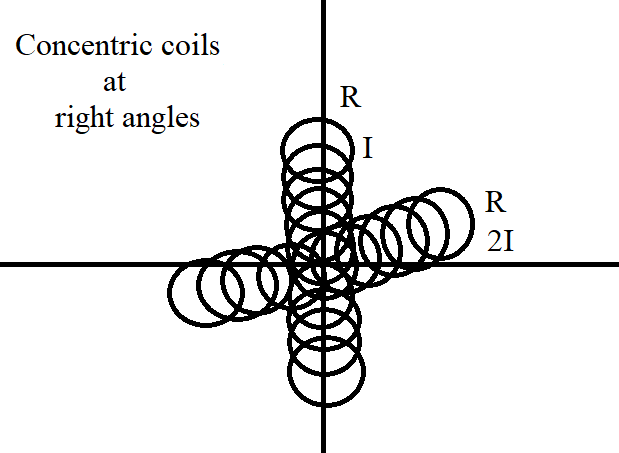
From Biot-Savart law, we know that magnetic field induction at the centre of a current carrying coil is given by
${{B}_{centre}}=\dfrac{{{\mu }_{0}}I}{2R}$
where
${{B}_{centre}}$ is the magnetic field induction at the centre of a coil
${{\mu }_{0}}$ is the magnetic constant of permeability in free space
$I$ is the current flowing through the coil
$R$ is the radius of the coil
Let this be equation 1.
From the question, we are provided that currents flowing in both the coils of same radius $R$ are $I$ and $2I$ respectively. Let the magnetic field induction at the centre due to the first coil be ${{B}_{c1}}$ and the magnetic field induction at the centre due to the second coil be ${{B}_{c2}}$. Let the total magnetic field at the common centre due to both the coils be ${{B}_{total}}$. It is clear that the total magnetic induction at the common centre is nothing but the resultant magnetic field due to both the coils and is given by
${{B}_{total}}=\sqrt{{{B}_{c1}}^{2}+{{B}_{c2}}^{2}}$
Let this be equation 2.
Applying equation 1 in both the coils, we have
${{B}_{c1}}=\dfrac{{{\mu }_{0}}I}{2R}$
where ${{B}_{c1}}$ is the magnetic induction at the common centre due to the coil through which a current $I$flows. Let this be equation 3.
${{B}_{c2}}=\dfrac{{{\mu }_{0}}(2I)}{2R}$
where ${{B}_{c2}}$ is the magnetic induction at the common centre due to the coil through which a current $2I$ flows. Let this be equation 4.
Observing both the equations above clearly, it is seen that
${{B}_{c2}}=2{{B}_{c1}}$
Let this be equation 5.
Now, the resultant magnetic induction at the common centre due to both the coils (equation 1) can be expressed as
${{B}_{total}}=\sqrt{{{B}_{c1}}^{2}+{{B}_{c2}}^{2}}=\sqrt{{{({{B}_{c1}})}^{2}}+{{(2{{B}_{c1}})}^{2}}}=\sqrt{5{{B}_{c1}}^{2}}=\sqrt{5}{{B}_{c1}}$
Substituting the value of ${{B}_{c1}}$ from equation 3 in the above equation, we have
${{B}_{total}}=\sqrt{5}{{B}_{c1}}=\sqrt{5}\dfrac{{{\mu }_{0}}I}{2R}$
Therefore, the resultant magnetic field induction at the centre is given by
${{B}_{total}}=\sqrt{5}\dfrac{{{\mu }_{0}}I}{2R}$

So, the correct answer is “Option C”.

Note:
The magnetic field induction at a point on the axis of a coil is different from the magnetic field induction at the centre of the coil. Magnetic field induction at a point on the axis of a coil is given by
${{B}_{axis}}=\dfrac{{{\mu }_{0}}I{{R}^{2}}}{2{{({{R}^{2}}+{{x}^{2}})}^{\dfrac{3}{2}}}}$
where $x$ is the distance of the point on the axis from the centre of coil.
Students can expect questions on this equation too. It is important to remember both the equations of magnetic field induction at the centre as well as a point on the axis to crack the questions on magnetic induction in a coil, easily.