Question

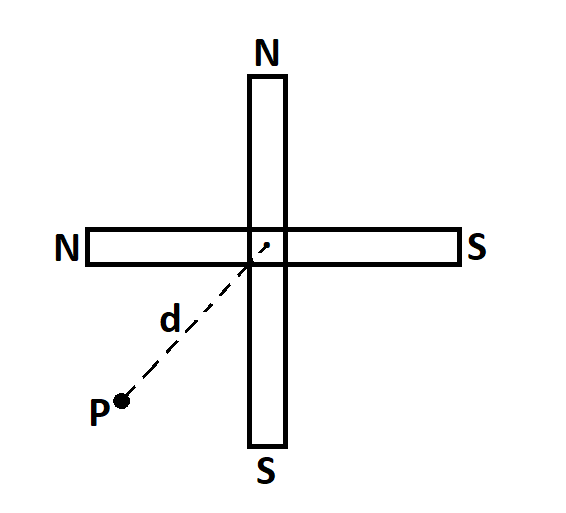
Two short magnets of equal dipole moments $M$ are fastened perpendicularly at their centers are given in the figure. The magnitude of the magnetic field at a distance $d$ from the center on the bisector of the right angle is

Answer 1

Hint: We will find the magnetic field at a distance $d$ from the center on the bisector of the right angle using the formula of magnetic field intensity by a short magnet at a point situated on the equatorial axis of the magnet. The resultant magnetic field will be the algebraic sum of magnetic fields due to the individual magnet.

Formula used:
${{\overrightarrow{B}}_{\text{axial}}}=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{2M\overrightarrow{r}}{{{\left( {{r}^{2}}-{{l}^{2}} \right)}^{2}}}$
${{\overrightarrow{B}}_{\text{equitorial}}}=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{M\overrightarrow{r}}{{{\left( {{r}^{2}}-{{l}^{2}} \right)}^{2}}}$

Complete step by step answer:
A magnetic field is a vector field that describes the magnetic influence on an electric charge of other moving charges or magnetized materials. A charge that is moving in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field.
A moment of a magnet may be a limited case of a closed-loop system of electrical current or a pair of poles because the size of the source is reduced to zero while keeping the magnetic moment constant. The magnetic field around any magnetic source looks increasingly just like the field of a dipole as the distance from the source increases.
A moment may be a measurement of the separation of two opposite electrical charges. Dipole moments are vector quantities. The magnitude is equal to the charge multiplied by the space between the fees and the direction for dipole moment is from negative charge to positive charge.
The magnetic field at a point on the axis line due to a short bar magnet is equal to the resultant of the magnetic fields due to the North pole and South pole of magnet.
${{\overrightarrow{B}}_{\text{axial}}}=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{2M\overrightarrow{r}}{{{\left( {{r}^{2}}-{{l}^{2}} \right)}^{2}}}$

The magnetic field at a point on the equatorial axis due to a short magnet is equal to the resultant of the magnetic fields due to the North Pole and South Pole of magnet.

${{\overrightarrow{B}}_{\text{equitorial}}}=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{M\overrightarrow{r}}{{{\left( {{r}^{2}}-{{l}^{2}} \right)}^{2}}}$
For short magnets,
${{\overrightarrow{B}}_{\text{axial}}}=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{2M\overrightarrow{r}}{{{r}^{4}}}$
${{\overrightarrow{B}}_{\text{equitorial}}}=\dfrac{{{\mu }_{o}}}{4\pi }\dfrac{M\overrightarrow{r}}{{{r}^{4}}}$
We are given that two short magnets of equal dipole moments $M$ are fastened perpendicularly at their centers and we have to calculate the magnitude of the magnetic field at a distance $d$ from the center on the bisector of the right angle.
The magnetic field at $P$ due to horizontal magnet above its midpoint,
${{B}_{1}}=\dfrac{{{\mu }_{o}}M}{4\pi {{d}^{3}}}$
The magnetic field at $P$ due to vertical magnet above its midpoint,
${{B}_{2}}=\dfrac{{{\mu }_{o}}M}{4\pi {{d}^{3}}}$
Hence, the net magnetic field at point $P$,
$B=\sqrt{B_{1}^{2}+B_{2}^{2}}=\dfrac{{{\mu }_{o}}\sqrt{2}M}{4\pi {{d}^{3}}}$

Note: While calculating the magnetic field, the direction of the field vector should be considered. Resultant magnetic field at a point due to various magnets is the algebraic sum of magnetic fields due to the individual magnet. Axial axis is the line joining two charges and passing through the centre of the dipole. Equatorial axis the line passing through the centre of dipole and perpendicular to the axial line.