Question

Two point charges $ - 8nC$ and $16nC$ are placed at corners of the side CD of a square ABCD having sides equal to $0.04m$. Find the electric field strength at point B.

Answer 1

Hint:Here, you are asked to find the electric field at a point due to two point charges. In order to answer this question, first what you need to do is find the electric field due to a point charge at the point of interest. After knowing the electric field, using that expression you can find the electric field at point B due to each charge individually and then use the superposition theorem.

Complete step by step answer:
Let us consider a single point charge having a charge equal to ${q_1}$ and this point charge is placed at the origin, for our ease, we have considered the charge to be positive. Now, take another point charge having charge equal to ${q_2}$, placed at some position vector $\overrightarrow r $. It is observed that the charge ${q_1}$ exerts a force on charge ${q_2}$.

This force is given by Coulomb’s law and is expressed as $\overrightarrow F = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_1}{q_2}}}{{{r^2}}}\widehat r$, where $\widehat r$ is the unit position vector. Now, electric field is defined as force per unit charge. Here, the ${q_2}$ is test charge, and therefore, electric field at the position vector $\overrightarrow r $ is given as $\overrightarrow E = \dfrac{{\overrightarrow F }}{{{q_2}}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_1}}}{{{r^2}}}\widehat r$. In terms of magnitude, electric field is $E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_1}}}{{{r^2}}}$.

Let us come back to out question, the situation is as shown in the figure:

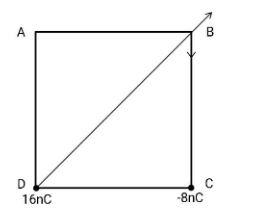
The direction of the electric field is shown in the figure. Let us find electric fields due to individual charge.
${E_{16nC}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_{16nC}}}}{{{{\left( {\sqrt 2 d} \right)}^2}}}\left( {\dfrac{{\widehat i + \widehat j}}{{\sqrt 2 }}} \right) \\
\Rightarrow{E_{16nC}} = \left( {9 \times {{10}^9}} \right)\dfrac{{\left( {16 \times {{10}^{ - 9}}} \right)}}{{{{\left( {\sqrt 2 \times 0.04} \right)}^2}}}\left( {\dfrac{{\widehat i + \widehat j}}{{\sqrt 2 }}} \right) \\
\Rightarrow{E_{16nC}} = 3.182 \times {10^4}\left( {\widehat i + \widehat j} \right) \\ $
\[\Rightarrow{E_{ - 8nC}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_{ - 8nC}}}}{{{d^2}}}\left( {\widehat j} \right) \\
\Rightarrow{E_{ - 8nC}} = \left( {9 \times {{10}^9}} \right)\dfrac{{\left( { - 8 \times {{10}^{ - 9}}} \right)}}{{{{\left( {0.04} \right)}^2}}}\left( {\widehat j} \right) \\
\Rightarrow{E_{ - 8nC}} = - 4.5 \times {10^4}\widehat j \\ \]
Now, according to the superposition theorem, the electric field at point B will be the vector sum of both the electric fields.
\[{E_B} = 3.182 \times {10^4}\widehat i + 3.182 \times {10^4}\widehat j + \left( { - 4.5 \times {{10}^4}} \right)\widehat j \\
\Rightarrow{E_B} = 3.182 \times {10^4}\widehat i - 1.318 \times {10^4}\widehat j \\
\therefore{E_B} = 3.44 \times {10^4}N{C^{ - 1}} \\ \]
Therefore, the electric field strength at point B is \[3.44 \times {10^4}N{C^{ - 1}}\].

Note:We have used Coulomb's law in order to find the electric field due to a point charge at the point of interest, so keep this in mind. Also, remember that the electric field due to positive charge is directed away from it and that due to negative charge is directed towards it, that is why the electric field arrow at point B due to negative charge is pointing in the downward direction.