Question

Two point charges +q and +q are fixed at (a,0,0) and (-a,0,0). A third point charge –q is at origin. State whether its equilibrium is stable, unstable or neutral if it is slightly displaced along y-axis.
A. stable
B. unstable
C. neutral
D. data insufficient

Answer 1

Hint: The state of equilibrium of the third charge will depend on the net force on it due to the other charges. As long as the net force remains zero, the charge will remain in the stable equilibrium and the charges will remain stationary.

Formula used:
The electrostatic force between two charges ${q_1}$ and ${q_2}$ is given by the Coulomb’s law by the following expression:
$F = \dfrac{1}{{4\pi { \in _0}}}\dfrac{{{q_1}{q_2}}}{{{r^2}}}$
Here r signifies the distance of charge from the point of observation and value of $\dfrac{1}{{4\pi { \in _0}}} = 9 \times {10^9}N{m^2}{C^{ - 2}}$

Detailed step by step solution:
At first, we have the three charges in the following configuration. We notice that the charges +q and +q are at equal distances from the charge –q. Using the expression for Coulomb law, we see that the force on charge –q due to the other two charges is equal and opposite. The net force can be written as follows using the expression for Coulomb’s law for force between two charges.
$\overrightarrow {{F_{net}}} = \overrightarrow F + \overrightarrow F = \dfrac{1}{{4\pi { \in _0}}}\dfrac{{{q^2}}}{{{a^2}}} - \dfrac{1}{{4\pi { \in _0}}}\dfrac{{{q^2}}}{{{a^2}}} = 0$

Now if we start displacing the charge –q along the y-axis, we notice that the distance from the other two charges will increase but the magnitude of their forces will remain the same as we can see in the following diagram.

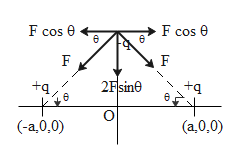
The forces acting on the charge –q will be resolved into horizontal and vertical components. Since the two positive charges have the same magnitude they will exert the same force on –q. Due to which, the horizontal components will cancel each other and while the vertical components will add up and the net force on –q will be given as
${F_{net}} = 2F\cos \theta $
We see that the force is not zero hence, there will be motion of charge –q towards the origin back to the stable equilibrium. Therefore the correct answer is option A because displacing the charge along the y-axis does not bring instability to the system.

Note: The student should note that when the charge –q is moving at some angle with respect to the other charges then the net force on the charge decreases with the increase in angle. Only the vertical component contributes to the force on the charge.