Question

Two plane mirror ${{M}_{1}}$ and ${{M}_{2}}$ have a length of $2\text{ m}$ each and are $10\text{ cm}$ apart. A ray of light is incident on one end of the mirror ${{M}_{2}}$ at an angle of $30{}^\circ $. The number of reflections light undergoes before reaching the other end is then.

Answer 1

Hint: To solve these types of questions we first have to find out the horizontal distance that the light ray travels before being incident on another plane mirror and then eventually calculate the number of such reflections made by the light ray to final reach the end of the plane mirror.

Complete step-by-step solution:
Let us assume that the light ray travels a horizontal distance $x$ after reflecting from mirror ${{M}_{2}}$ and being incident on mirror ${{M}_{1}}$ and the angle of incidence of the light ray be $\theta $. For better understanding look at the figure:

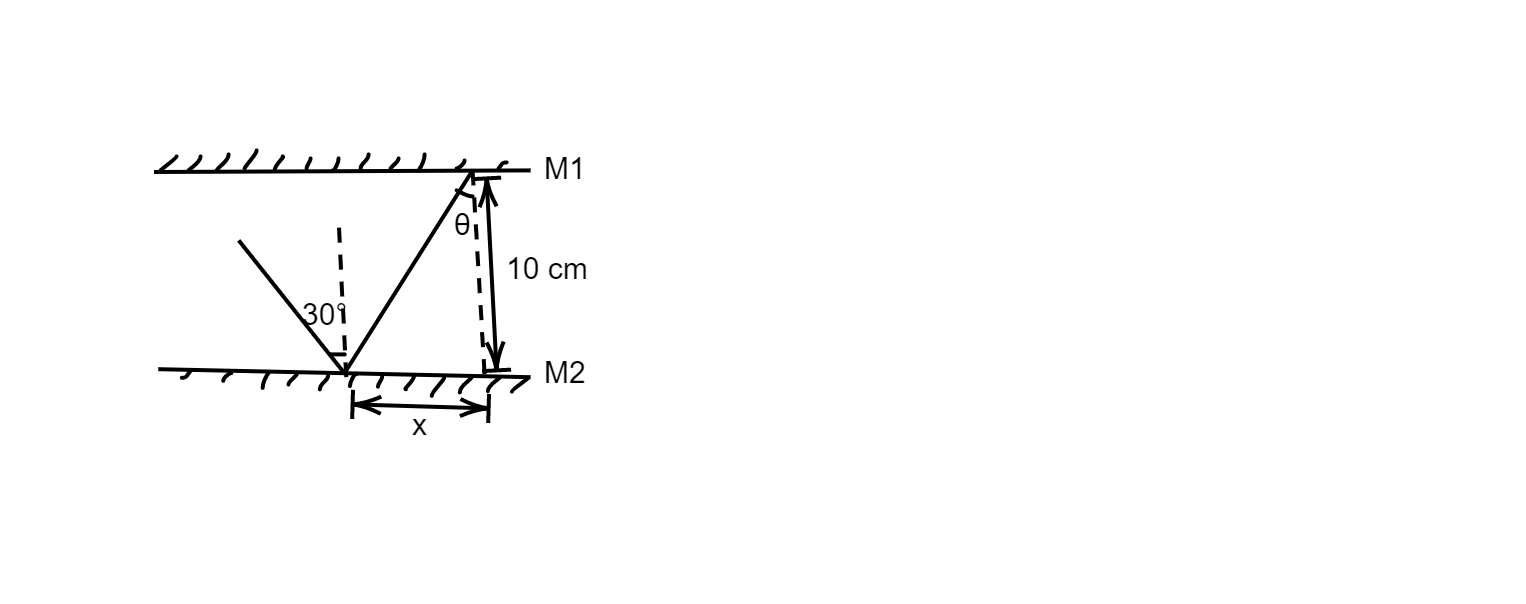
Now, we know that the plane mirrors ${{M}_{1}}$ and ${{M}_{2}}$ have a length of $2\text{ m}$ each and are $10\text{ cm}$ apart. Hence from observing the figure, we can write down that:
\[\tan \theta =\dfrac{x}{10}\]
Now, we know that the angle of incidence and angle of reflection are equal in case of reflection from a plane mirror, hence the angle of reflection of the light ray when reflected from mirror ${{M}_{2}}$ will be $30{}^\circ $ and thus the angle of incidence of the light ray when the light ray is incident on mirror ${{M}_{1}}$ will also be $30{}^\circ $ which makes $\theta =30{}^\circ $. On substituting the values in the equation, we get:
\[\begin{align}
  & \tan 30{}^\circ =\dfrac{x}{10} \\
 & \Rightarrow x=10\tan 30{}^\circ \\
 & \Rightarrow x=\dfrac{10}{\sqrt{3}}\text{ cm} \\
\end{align}\]
Now, to calculate the total number of reflections that light undergoes before reaching the other end we will divide the value of total distance that the light ra has to cover to reach the end by the distance that light rays travels in one reflection. Hence the total number of reflections will be:
$\begin{align}
  & n=\dfrac{200}{\dfrac{10}{\sqrt{3}}} \\
 & \Rightarrow n=\dfrac{200\sqrt{3}}{10} \\
 & \therefore n=20\sqrt{3} \\
\end{align}$

Note: To solve these types of questions, we need to remember the basic rules of reflection like the angle of incidence made by the incident light with the normal is equal to the angle of reflection that the reflected ray after reflection makes with the normal.