Question

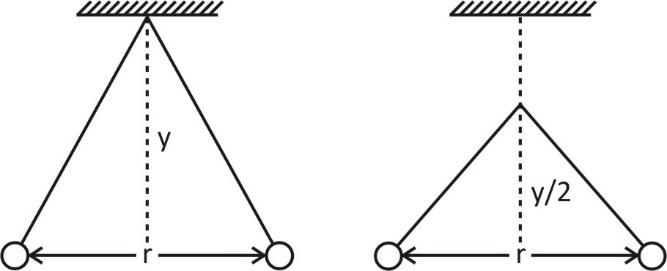
Two pith balls carrying equal charges are suspended from a common point by strings of equal length, the equilibrium separation between them is $r$ . Now the strings are rigidly clamped at half the height. The equilibrium separation between the balls now become

A. ${\left( {\dfrac{1}{{\sqrt 2 }}} \right)^2}$
B. $\left( {\dfrac{r}{{\sqrt[3]{2}}}} \right)$
C. $\left( {\dfrac{{2r}}{{\sqrt 3 }}} \right)$
D. $\left( {\dfrac{{2r}}{3}} \right)$

Answer 1

Hint: Here we have to first find the forces along different directions along with the horizontal and vertical components. Then we have to equate the force s and find the equilibrium separation between the balls.

Complete step by step answer:
Given,
Two pith balls carrying equal charges are suspended from a common point by strings of equal length, the equilibrium separation between them is $r$ . Now the strings are rigidly clamped at half the height.

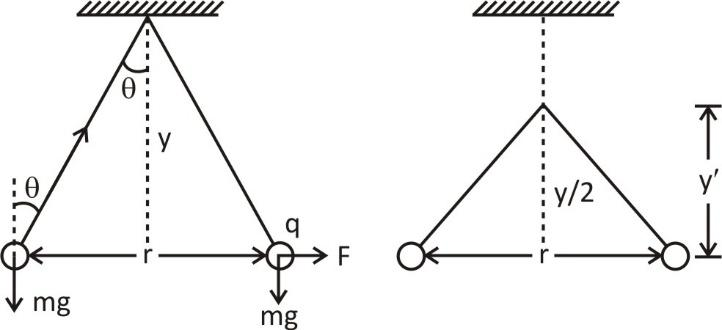
Let charge $q$ be acting on the balls with force $F$ . Let the angle be $\theta $ . Let weight $mg$ be acting downwards on both the balls of the pendulum.
Therefore,
 $
  T\cos \theta = mg \\
  T\sin \theta = F \\
  \tan \theta = \dfrac{F}{{mg}} \\
 $
Also $\tan \theta = \dfrac{r}{{2y}}$ (from the diagram)
So,
  $
  \tan \theta = \dfrac{F}{{mg}} \\
\implies \dfrac{r}{{2y}} = \dfrac{F}{{mg}} \\
\implies \dfrac{r}{{2y}} = \dfrac{{\dfrac{{k{q^2}}}{{{r^2}}}}}{{mg}} \\
\implies y = k{r^3} \\
 $
Let the length for the second figure be $y'$
Similarly we can get-
$y' = kr{'^3}$
So,
$
\dfrac{y}{{y'}} = {\left( {\dfrac{r}{{r'}}} \right)^3} \\
\implies \dfrac{r}{{r'}} = {\left( {\dfrac{y}{{y'}}} \right)^{1/3}} \\
\implies r' = r{\left( {\dfrac{{y'}}{y}} \right)^{1/3}} \\
\implies r' = r{\left( {\dfrac{y}{{2y}}} \right)^{1/3}} \\
\therefore r' = \dfrac{r}{{{2^{1/3}}}} \\
$

So, the correct answer is “Option D”.

Additional Information:
It is helpful to manage forces acting at any angle from the alignment axes into mutually perpendicular forces called components. The portion of the force parallel to the x-axis is called the x-component, the y-component is parallel to the y-axis.
The resultant force is the single force produced by integrating a system of forces and torques acting on a rigid body and the corresponding torque. The main characteristic of the resulting force, or the resulting force-torque, is that it has the same effect as the initial force mechanism on the rigid body.

Note:
Sometimes to find the components of force we use $F = mg\cos \theta $ and sometimes we use $F\cos \theta = mg$ . Here we have used $F\cos \theta = mg$ as the ball of the pendulum is supposed to be hanging in air. Also we have to find $\tan \theta $ from the diagram given correctly.