Question

Two parallel plane mirrors ${M_1}$and ${M_2}$ have a length of $20m$ each and are $10cm$ apart. A ray of light is incident on one end of the mirror ${M_2}$ at an angle ${53^o}$. Calculate the number of times the ray undergoes reflections
1. If the last reflection is at the other edge of the mirror.
2. Before it reaches the other end (given $\tan {53^ \circ } = \dfrac{4}{3}$)

Answer 1

Hint: Draw ray diagram of all the images formed using the laws of reflection reflected rays will go back and forth in both the mirrors until ray comes out of the mirror.

Complete step by step answer:
Mirrors are $10cm$ apart, incident ray starts from one end of the mirror ${M_2}$ at an angle of ${53^o}$ and length of each mirror is $20m$
If we draw the ray diagram it will look like this

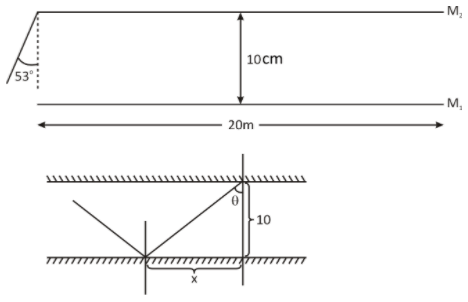
The distance travelled by incident ray along the length of the mirror in one reflection is denoted by x
And $\tan \theta = \dfrac{x}{{10cm}}$ where $\theta $ is ${53^ \circ }$
Therefore, $\tan {53^ \circ } = \dfrac{4}{3} = \dfrac{x}{{10}} \Rightarrow x = \dfrac{{40}}{3}cm = \dfrac{4}{{30}}m$
Now, $total \, number\, of\,reflections = \dfrac{{length\,of\,the\,mirror}}{x}
\Rightarrow n = \dfrac{{20}}{{\dfrac{4}{{30}}}} = 150$
If we consider the last image at the edge of the mirror we will get 150images
Else if we don’t consider the last image at the edge we will get 149 images
Hence, Answer for part(1) will be 150 And Answer for part(2) will be 149.

Note:
To solve such types of questions you need to find the distance travelled by the reflected ray along the length of the mirror and then divide with the total length of the mirror to get the final answer Also, you should always check for the last reflected ray’s position like here it is formed at the very edge and your answer will vary depending upon whether or not you consider the image at the edge.