Question

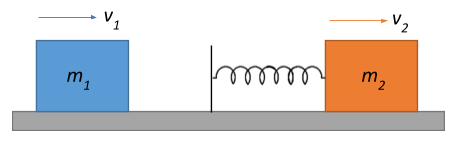
Two masses $m_1=2\;kg$ and $m_2=5\;kg$ are moving on a frictionless surface with velocities $10\;ms^{-1}$ and $3\;ms^{-1}$ respectively. $m_2$ is ahead of $m_1$. An ideal spring of spring constant $k=1120\;Nm^{-1}$ is attached on the back side of $m_2$. The maximum compression of the spring will be

A. 0.51 m
B. 0.062 m
C. 0.25 m
D. 0.72 m

Answer 1

Hint: Obtain expressions for the initial and final momenta and energy for the system. Remember to account for the kinetic energy of the masses and the (kinetic) potential energy of the spring for the final energy. First use the law of conservation of momentum to find the combined velocity with which the masses move under maximum compression. Then use the law of conservation of energy to arrive at equations that you can arithmetically solve after plugging in the given values to obtain the value for the maximum compression of the spring.

Formula Used:
Linear momentum $p=mv$
Kinetic energy $KE = \dfrac{1}{2}mv^2$
Spring potential energy $PE = \dfrac{1}{2}kx^2$

Complete Step-by-Step Solution:
Let us first consider the initial condition where we have masses $m_1=2\;kg$ and $m_2=5\;kg$ moving on a frictionless surface with velocities $10\;ms^{-1}$ and $3\;ms^{-1}$ respectively.

Their individual momenta will be:
$p_1 = m_1v_1 = 2\times 10 = 20\;kgms^{-1}$
$p_2 = m_2v_2 = 5\times 3 = 15\;kgms^{-1}$

And their individual energies by virtue of their motion will be:
$E_1 = \dfrac{1}{2}m_1v_1^2 = \dfrac{1}{2} \times 2 \times 10^2 = 100\;J$
$E_2 = \dfrac{1}{2}m_2v_2^2 = \dfrac{1}{2} \times 5 \times 3^2 = 22.5\;J$

Therefore, the initial momentum of the entire system will be $p_i = p_1+p_2 = 20+15 = 35\;kgms^{-1}$

And the initial total energy of the system will be $E_i = E_1+E_2 = 100+22.5=122.5\;J$

Now, at the time of maximum compression, the two masses act like they are clumped together and move with a common velocity, say $v$.

The final momentum of the system will be $p_f = (m_1+m_2)v = (2+5)v = 7v\;kgms^{-1}$

The final energy of the system will be the sum of the masses’ collective kinetic energy and the potential energy of the spring (of spring constant $k =1120\;Nm^{-1}$) under a maximum compression, say x, i.e.,

$E_f = \dfrac{1}{2}(m_1+m_2)v^2 + \dfrac{1}{2}kx^2 = \dfrac{1}{2}(2 +5)v^2 +\dfrac{1}{2} \times 1120 \times x^2 =\dfrac{7}{2}v^2+ 560x^2\;J$

Now, from the law of conservation of momentum, we know that the total momentum of the system remains constant throughout, i.e.,
$p_i = p_f$
$\Rightarrow 35 = 7\;v \Rightarrow v = \dfrac{35}{7} = 5\;ms^{-1}$

Similarly, the law of conservation of energy states that the total energy of an isolated system remains constant and is conserved over time, i.e.,
$E_i = E_f$
$\Rightarrow 122.5 =\dfrac{7}{2}v^2+ 560x^2$
Plugging in $v= 5\;ms^{-1}$,
$122.5 = \dfrac{7}{2}\times 5^2 +560x^2$
$\Rightarrow 122.5 = 87.5 +560x^2$
$\Rightarrow 122.5-87.5 = 560x^2$
$\Rightarrow 560x^2=35$
$\Rightarrow x^2 = \dfrac{35}{560} = \dfrac{1}{16}$
$\Rightarrow x = \sqrt{\dfrac{1}{16}} = \dfrac{1}{4} = 0.25\;m$

Therefore, the correct choice will be C. 0.25 m.

Note:
Remember that the spring constant remains the same for a given spring within its elastic limit. It is essentially the force applied if the displacement in the spring is unity. It is important to understand that force and displacement follow a linear relation, i.e., a graph between force and displacement would yield a straight line since successive increments in the force applied would produce increments in extension/compression by a common factor, which we call as the spring “constant”.