Question

Two masses ${{m}_{1}}$ and ${{m}_{2}}$, ${{m}_{1}}>{{m}_{2}}$ move in circular paths under the action of their gravitational attraction. While doing so, their separation remains constant and equals $'r'$. Radius of circular path of ${{m}_{2}}$ is:
(A). $\dfrac{r}{2}$
(B). $\dfrac{{{m}_{1}}}{{{m}_{2}}}r$
(C). $\dfrac{{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}r$
(D). $\dfrac{{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}r$

Answer 1

Hint: Two particles revolve around a point due to the mutual gravitational force of attraction. This means they are revolving around their centre of mass. The radius of their circular paths is the distance from the centre of mass. The centre of mass will be at a point where mass distribution is constant.

Formulas used:
${{m}_{1}}{{r}_{1}}={{m}_{2}}{{r}_{2}}$
$d={{r}_{1}}+{{r}_{2}}$

Complete step-by-step solution:
Since the particles are moving under the action of mutual gravitational attraction, they are revolving around their centre of mass.
The centre of mass of a system is the point at which the whole mass of the system is assumed to be concentrated.
The separation between the masses is given as $r$

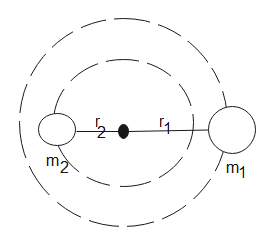
From the above figure,
$d={{r}_{1}}+{{r}_{2}}$ - (1)
Here, ${{r}_{1}}$ is the radius of ${{m}_{1}}$ or its distance from centre of mass
${{r}_{2}}$ is the radius of particle ${{m}_{2}}$ or its distance from centre of mass
Since, the mass of one particle is greater than the other mass distribution is not equal. The centre of mass will be closer to the bigger mass.
The centre of mass will be at a point where,
${{m}_{1}}{{r}_{1}}={{m}_{2}}{{r}_{2}}$
$\Rightarrow {{r}_{2}}=\dfrac{{{m}_{1}}}{{{m}_{2}}}{{r}_{1}}$ - (2)
From eq (1), we have,
$\begin{align}
  & d={{r}_{1}}+{{r}_{2}} \\
 & \Rightarrow {{r}_{1}}=d-{{r}_{2}} \\
\end{align}$
Substituting in eq (2), from the above equation, we get,
$\begin{align}
  & {{r}_{2}}=\dfrac{{{m}_{1}}}{{{m}_{2}}}(d-{{r}_{2}}) \\
 & \Rightarrow {{r}_{2}}=d\dfrac{{{m}_{1}}}{{{m}_{2}}}-{{r}_{2}}\dfrac{{{m}_{1}}}{{{m}_{2}}} \\
 & \Rightarrow {{r}_{2}}(1+\dfrac{{{m}_{1}}}{{{m}_{2}}})=d\dfrac{{{m}_{1}}}{{{m}_{2}}} \\
 & \Rightarrow {{r}_{2}}(\dfrac{{{m}_{1}}+{{m}_{2}}}{{{m}_{2}}})=d\dfrac{{{m}_{1}}}{{{m}_{2}}} \\
 & \therefore {{r}_{2}}=\dfrac{{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}d \\
\end{align}$

Therefore, the magnitude of the radius or the distance from the centre of mass of ${{m}_{2}}$ is $\dfrac{{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}d$.

Hence, the correct option is (D).

Note:
The nature of gravitational forces is always attractive. The position of centre of mass depends on the distribution of mass of the system. If both masses were equal, the centre of mass would be in the centre. The radius of the particles of the system is inversely proportional to their masses.