Question

Two masses A and B of 10Kg and 5Kg respectively are being connected with a string passing over a frictionless pulley at a corner of a table. The coefficient of friction of A with the table is $0.2$. The minimum mass of C that should be placed over A to prevent it from moving is equal to? Show it in a neat diagram.

Answer 1

Hint: First of all draw the diagram as per the condition mentioned in the question. Then find out all the forces which are acting over the two masses in all possible ways. Sometimes the resultant mass or the combination of two masses should be used up in order to solve this question.

Complete step by step answer:
First of all, let us make a clear cut idea about the question in which two masses are connected using a wire or a string passing over a pulley. We have to place a mass above the mass A in order to prevent the movement of the whole system. So let us show it in a diagram first.

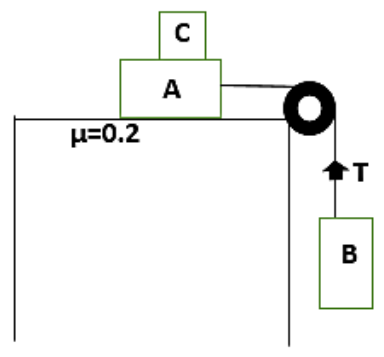
Now as mentioned in the question, the mass of block A is given as,
${{M}_{A}}=10Kg$
And the mass of block B is given as,
${{M}_{B}}=5Kg$
Coefficient of friction between the table and the block A,
$\mu =0.2$
Now let us find out the tension of the string.
$T={{M}_{B}}g$
Where $g$the acceleration due to gravity.
Substituting the values in the equation will give,
$T=5\times 10=50N$
Now let us consider the combination of the two masses A and C,
Resultant mass will be,
\[{{M}_{AC}}=\left( 10+{{M}_{C}} \right)\]
Then the tension over the string can be written as,
$\begin{align}
  & T=\mu R \\
 & T=0.2\times \left( 10+{{M}_{C}} \right)g \\
\end{align}$
Let us compare this equation with the above mentioned tension’s value,
$T=0.2\times \left( 10+{{M}_{C}} \right)g=50N$
Simplifying the terms,
$\begin{align}
  & 50=0.2\times 100+0.2\times {{M}_{c}}\times 10 \\
 & 50-20=2{{M}_{c}} \\
 & {{M}_{c}}=15Kg \\
\end{align}$
Hence the mass of block C is
 ${{M}_{c}}=15Kg$
Therefore the correct answer for the question is obtained.

Note: The coefficient of friction is described as the ratio of the force needed to move the sliding surfaces over each other. A coefficient of friction more than one means the frictional force has been stronger than the normal force. An object such as silicone is having a coefficient of friction greater than one.