Question

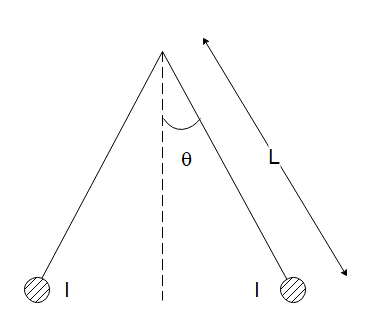
Two long current carrying thin wires, both with current , are held by insulating threads of length $ L $ and are in equilibrium as shown in the figure, with threads making an angle $ \theta $ with the vertical. If wires have a mass per unit length $ \lambda $ then the value of $ I $ is:
(g = gravitational acceleration) $ I $

A) $ \sin \theta \sqrt {\dfrac{{\pi \lambda gL}}{{{\mu _0}\cos \theta }}} $
B) $ 2\sin \theta \sqrt {\dfrac{{\pi \lambda gL}}{{{\mu _0}\cos \theta }}} $
C) $ 2\sqrt {\dfrac{{\pi gL}}{{{\mu _0}}}\tan \theta } $
D) $ \sqrt {\dfrac{{\pi \lambda gL}}{{{\mu _0}}}\tan \theta } $

Answer 1

Hint : In this solution, we will determine the force acting on the two wires due to the current flowing in them. Then we will use the components of force to determine the value of $ I $ .

Formula used: In this solution, we will use the following formula:
 $ F = \dfrac{{{\mu _0}{I_1}{I_2}L}}{{2\pi d}} $ where $ F $ is the force between two current-carrying wires having a current $ {I_1} $ and $ {I_2} $ , having the same length $ L $ and distance $ d $ between them.

Complete step by step answer
Let us start by drawing a free-body diagram of the force between the current-carrying cable.

As we can see, the forces balanced in the horizontal direction will be
 $ T\sin \theta = F $
And in the vertical direction will be
 $ T\cos \theta = mg $
Diving both these equations, we get
 $ \tan \theta = \dfrac{F}{{mg}} $
The mass of the strings can be determined as the product of the linear mass density and the length of the rod. So, we have
 $ m = \lambda L $
Now, the force between the two current-carrying cables $ ({I_1} = {I_2} = I) $ which are placed a distance $ 2L\sin \theta $ apart will be
 $ F = \dfrac{{{\mu _0}{I^2}L}}{{2\pi 2L\sin \theta }} $
Substituting the value of force in equation (1), we get
$ I = 2\sin \theta \sqrt {\dfrac{{\pi \lambda gL}}{{{\mu _0}\cos \theta }}} $ which corresponds to option (B).

Note
We must carefully infer from the diagram that the current-carrying cables are placed perpendicular to the plane of the page. Since we only want to find the magnitude of the force, the direction of the current in the cables is inconsequential to us.