Question

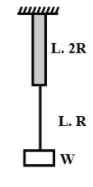
Two light wires made up of the same material (Young Modulus, Y) have length L each and radii R and 2R respectively. They are joined together and suspended from a rigid support. Now, a weight W attached to the free end of the joint wire as shown in the figure. Find the elastic potential energy stored in the system due to the extension of the wire.
          

Answer 1

Hint: Use the formula for elastic potential energy. Substitute strain in terms of stress. Calculate stress for both the wires. Substitute them in the formula and obtain potential energy for each wire. Add them and get the total elastic potential stored in the system.

Complete answer:
Given: Radii of two wires are R and 2R respectively
The elastic potential energy in the system is given by,
$V=\dfrac { 1 }{ 2 } \times stress\times strain\times L\times A$...(1)
But, $Y=\dfrac { stress }{ strain }$
Rearranging the above equation and substituting in equation.(1)
$\Rightarrow V=\dfrac { 1 }{ 2 } \times stress\times \dfrac { stress }{ Y } \times L\times A$...(2)
We know, $stress=\dfrac { W }{ A }$...(3)
Where, A: Area of cross-section
Substituting equation.(3) in equation.(2) we get,
$V=\dfrac { 1 }{ 2 } \times \dfrac { W }{ A } \times \dfrac { W }{ AY } \times L\times A$
$\Rightarrow V=\dfrac { 1 }{ 2 } \times \dfrac { { W }^{ 2 }L }{ AY }$...(4)
So, first we need to calculate the stress of both the wires.
Stress in the wire with radius R= $ \dfrac { W }{ \pi { R }^{ 2 } }$
Similarly, Stress in the wire with radius 2R= $ \dfrac { W }{ 4\pi { R }^{ 2 } }$
To get the potential energy for wire with radius R, substitute the values in equation.(4)
${ V }_{ 1 }=\dfrac { 1 }{ 2 } \times \dfrac { { W }^{ 2 }L }{ \pi { R }^{ 2 }Y }$
Similarly, for the wire with radius 2R,
${ V }_{ 2 }=\dfrac { 1 }{ 2 } \times \dfrac { { W }^{ 2 }L }{ 4\pi { R }^{ 2 }Y }$
Therefore, the total elastic potential energy is,
$V={ V }_{ 1 }+{ V }_{ 2 }$
Substituting the values in above equation we get,
$ V=\dfrac { 1 }{ 2 } \dfrac { { W }^{ 2 }L }{ \pi { R }^{ 2 }Y } +\dfrac { 1 }{ 2 } \dfrac { { W }^{ 2 }L }{ 4\pi { R }^{ 2 }Y }$
$\Rightarrow V=\dfrac { { 5W }^{ 2 }L }{ 8\pi { R }^{ 2 }Y }$
Hence, the elastic potential energy stored in the system due to the extension of the wire is $ \dfrac { { 5W }^{ 2 }L }{ 8\pi { R }^{ 2 }Y }$

Note:
Young’s modulus describes the stiffness of a material. Greater the Young modulus, higher is the stiffness. Higher the stiffness, greater is the amount of load to be put to change the shape of the material. For material with lower Young modulus, less load is to be put on the material to change its shape.