Question

Two identically charged spheres are suspended by strings of equal length. When they are immersed in kerosene, the angle between their strings remains the same as it was in the air. Find the density of the spheres. The dielectric constant of kerosene is 2 and its density is \[800kg{m^{ - 3}}\].

Answer 1

Hint: To simplify the problem, draw a diagram for the problem and show the forces acting on the spheres. In equilibrium position all the forces acting the sphere will cancel each other, use this concept to find out the density of the spheres.

Complete step by step answer:
Given, dielectric constant of kerosene, \[k = 2\]
Density of kerosene, \[{\rho _{\text{k}}} = 800kg{m^{ - 3}}\]
Let us draw a diagram showing the forces acting on two spheres A and B when the system is in air.

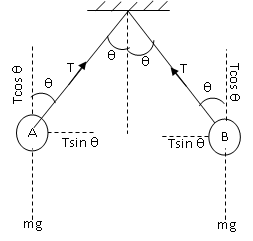
Let m be the mass of each sphere, \[2\theta \] be the angle between the two strings, T be the tension on each string and g is the acceleration due to gravity and F be the electrostatic force of repulsion between the two spheres acting horizontally.
For sphere A, in equilibrium position along vertical from the diagram we have,
\[T\cos \theta = mg\]..............\[(i)\]
And along horizontal from the diagram
\[T\sin \theta = F\]................\[(ii)\]
Diving \[(ii)\] by\[(i)\], we have
\[\tan \theta = \dfrac{F}{{mg}}\]................\[(iii)\]

When the balls are suspended in kerosene of density \[{\rho _{\text{k}}}\] and dielectric constant \[k\], the electrostatic force will then be \[{F'} = \dfrac{F}{k}\] and the weight of the sphere or the force acting downwards will be
\[m{g'} = mg - {\text{upthrust}}\,{\text{of}}\,{\text{kerosene}}\],
Upthrust of kerosene can be written as, \[{\text{upthrust = m}}\dfrac{{{\rho _k}}}{{{\rho _{ball}}}}g\]
Where \[{\rho _{ball}}\] is the density of each ball.
\[\therefore m{g'} = mg\left( {1 - \dfrac{{{\rho _k}}}{{{\rho _{ball}}}}} \right)\]
When the system is suspended in kerosene it is given the angle between them remains the same so equation \[(iii)\]can be written as
\[\tan \theta = \dfrac{{{F'}}}{{m{g'}}}\]
\[ \Rightarrow \tan \theta = \left( {\dfrac{F}{k}} \right)\dfrac{1}{{mg\left( {1 - \dfrac{{{\rho _k}}}{{{\rho _{ball}}}}} \right)}}\]
\[ \Rightarrow \tan \theta = \dfrac{F}{{mgk}}\dfrac{1}{{\left( {1 - \dfrac{{{\rho _k}}}{{{\rho _{ball}}}}} \right)}}\].................\[(iv)\]
Now, equation \[(iii)\] and \[(iv)\], we have
\[\dfrac{F}{{mgk}}\dfrac{1}{{\left( {1 - \dfrac{{{\rho _k}}}{{{\rho _{ball}}}}} \right)}} = \dfrac{F}{{mg}}\]
\[ \Rightarrow \dfrac{1}{{k\left( {1 - \dfrac{{{\rho _k}}}{{{\rho _{ball}}}}} \right)}} = 1\].............\[(v)\]
Now, putting the values of \[{\rho _k}\]and \[k\]in equation \[(v)\] we have,
\[ \Rightarrow \dfrac{1}{{2\left( {1 - \dfrac{{800}}{{{\rho _{ball}}}}} \right)}} = 1\]
\[ \Rightarrow {\rho _{ball}} = 2{\rho _{ball}} - 1600 \\
   \Rightarrow {\rho _{ball}} = 1600kg{m^{ - 3}} \\\]

Therefore, density of each sphere is \[1600kg{m^{ - 3}}\].

Note:
While solving such types of questions, we should carefully draw a neat diagram and show all the forces acting on the system. If we make mistakes while showing the forces acting on the system then it would affect the calculation part and could lead to wrong answers.