Question

Two identical wires A and B, each of length ‘l’, carrying the same current ‘i’. Wire A is bent into a circle of radius ‘R’ and wire B is bent to form a square of side ‘a’. If $B_A \ and \ B_B$ are the values of the magnetic field at the centre of the circle and square respectively, then the ratio $\dfrac{B_A}{B_B}$ is?

Answer 1

Hint: Magnetic field is the space around the magnet where the effect of magnet can be felt by another magnet or iron piece. Magnetic fields can also be produced by a moving charge whose intensity can be determined by the velocity and magnitude of charge. The S.I unit of magnetic field is Tesla (T) whereas the C.G.S unit is Gauss (G). The intensity of the magnetic field could be determined by applying Biot-savart law.
Formula used:
$B_{circle} = \dfrac{\mu_{\circ}i}{2R },\ B_{wire} = \dfrac{\mu_{\circ}i}{4\pi d}(sin \phi_1 + sin \phi_2)$

Complete answer:
Since moving charge produces magnetic field, hence current, which is also the flow of electrons, produces magnetic field around it. Due to a complete circular loop, the magnetic field at its centre is given by$B = \dfrac{\mu_{\circ}i}{2R }$ where $\mu_\circ$ is the permeability of free space. ‘R’ is the radius of a circular loop in which current ‘i’ is flowing.
Also, total length of wire = l i.e. circumference of wire = l.
$\implies 2\pi R = l$
$\implies R = \dfrac{l}{2\pi}$
Hence $B_A = \dfrac{\mu_{\circ}i}{2(\dfrac{l}{2\pi})} = \dfrac{\mu_\circ i\pi}{l}$
Now, magnetic field at the centre of the square:
Using $B_{wire} = \dfrac{\mu_{\circ}i}{4\pi d}(sin \phi_1 + sin \phi_2)$ where ‘d’ is the perpendicular distance of wire from the point having starting and final angles $\phi_1 \ and \ \phi_2$ respectively.

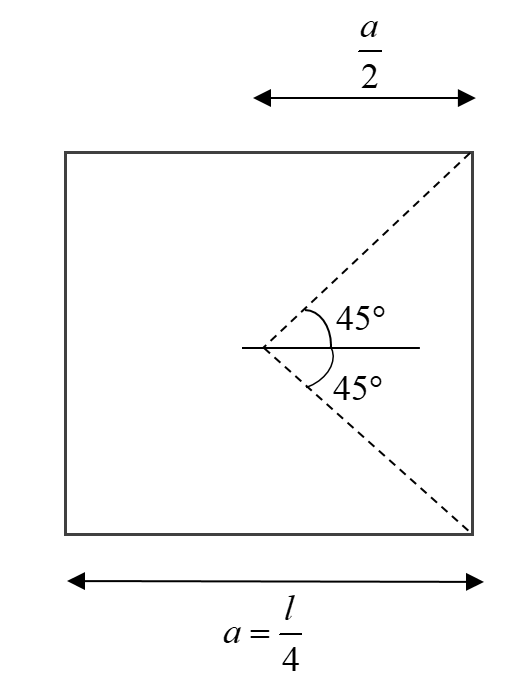
Thus $\phi_1 \ = \ \phi_2 = 45^{\circ}$and $d = \dfrac a2 = \dfrac l8$
Thus putting in$B_{wire} = \dfrac{\mu_{\circ}i}{4\pi d}(sin \phi_1 + sin \phi_2)$, we get;
$B = \dfrac{\mu_{\circ}i}{4\pi (\dfrac l8)}(sin 45\circ + sin 45\circ)$
$B = \dfrac{2\mu_{\circ}i}{\pi l}(2\times\dfrac{1}{\sqrt 2})$
$B = \dfrac{2\sqrt2\mu_{\circ}i}{\pi l}$
Now, this is the field due to one side of the square. Total field due to four side of the square = 4B
Thus $B_B = \dfrac{8\sqrt2 \mu_{\circ}i}{\pi l}$
Thus the ratio $\dfrac{B_A}{B_B} = \dfrac{ \dfrac{\mu_\circ i\pi}{l}} {\dfrac{8\sqrt2 \mu_{\circ}i}{\pi l}} = \dfrac{\pi^2}{8\sqrt2}$
Hence the ratio will be $\dfrac{\pi^2}{8\sqrt2}$

Note:
The term $\mu_{\circ}$, which is the permeability of free space has value $4\pi \times 10^{-7}m \ kgs^{-2}A^{-2} = 4\pi \times 10^{-7} H/m$, where H stands for henry, the unit of inductance. Student should take care of the fact that in case of straight wires, we have to calculate field for one wire and then multiply the field accordingly. But for a curved figure like a circle, we have the direct formula for the net field at the centre.