Question

Two identical non-relativistic particles $A$ and $B$ move at right angles to each other, processing de Broglie wavelengths ${\lambda _1}$ and ${\lambda _2}$ respectively. The de Broglie wavelength of each particle in their centre of mass frame of reference is
A) ${\lambda _1} + {\lambda _2}$
B) $\dfrac{{2{\lambda _1}{\lambda _2}}}{{\left( {\sqrt {{\lambda _1}^2 + {\lambda _2}^2} } \right)}}$
C) $\dfrac{{{\lambda _1}{\lambda _2}}}{{\left( {\sqrt {\left| {{\lambda _1}^2 + {\lambda _2}^2} \right|} } \right)}}$
D) $\dfrac{{\left( {{\lambda _1} + {\lambda _2}} \right)}}{2}$

Answer 1

Hint:The two particles are moving at right angle to each other, processing de Broglie wavelength. The velocity of the centre of mass can be derived using the vector form of two velocities and the velocity of the two particles with respect to the centre of mass velocity is derived. And by applying the de Broglie wavelength formula, to find the de Broglie wavelength of each particle in the centre of mass is derived.

Useful formula:
The velocity of centre of mass with respect to the two velocities,
${\vec v_c} = \dfrac{{{v_1}}}{2}\vec i + \dfrac{{{v_2}}}{2}\vec j$
Where, ${v_c}$ is the velocity of centre of mass, ${v_1}$ is the velocity of first particle, ${v_2}$ is the velocity of second particle, $\vec i$ and $\vec j$ are the direction vectors.

De Broglie wavelength, $\lambda = \dfrac{h}{{mv}}$
Where, $h$ is the Planck’s constant, $m$ is the mass of the particle and $v$ is the velocity of the particle.

Complete step by step answer:

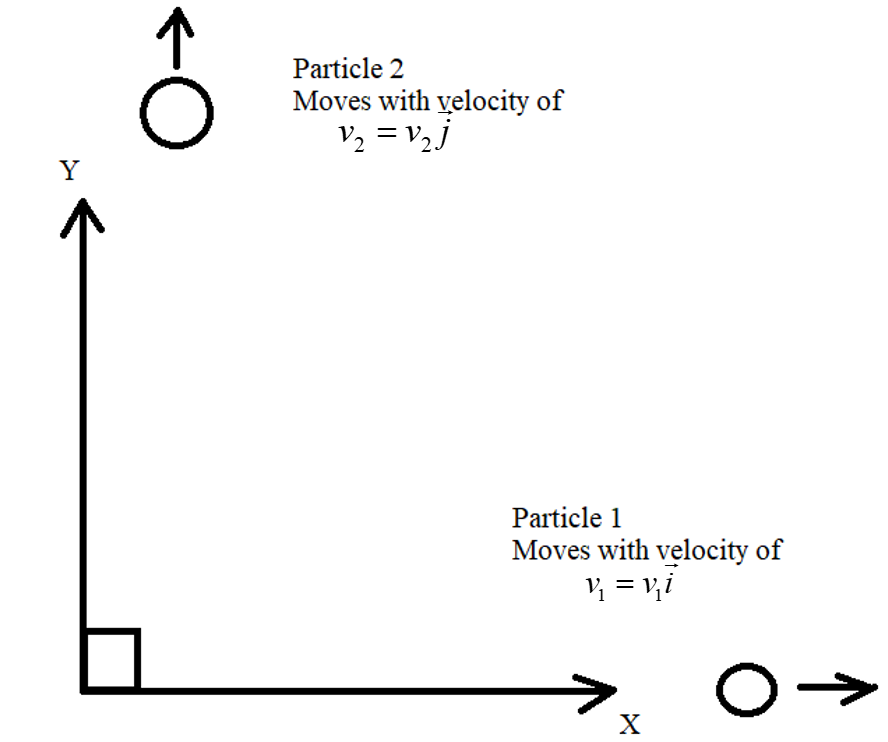
Assume that,
The velocity of the first particle is ${v_1} = {v_1}\vec i$
The velocity of the second particle is ${v_2} = {v_2}\vec j$
The wavelength of the first particle is ${\lambda _1}$
The wavelength of the second particle is ${\lambda _2}$

Thus, the velocity of the first particle with respect to centre of mass,
${v_{1c}} = {v_1} - {v_c}$
Substituting the value of ${v_1}$ and ${v_c}$ in above relation,
${v_{1c}} = {v_1}\vec i - \dfrac{{{v_1}}}{2}\vec i - \dfrac{{{v_2}}}{2}\vec j$
Performing the arithmetic operation on RHS of the equation, we get
$
  {v_{1c}} = \dfrac{{{v_1}}}{2}\vec i - \dfrac{{{v_2}}}{2}\vec j \\
  {v_{1c}} = \dfrac{{{v_1}\vec i - {v_2}\vec j}}{2} \\
 $
De Broglie wavelength of first particle with respect to centre of mass,
${\lambda _{1c}} = \dfrac{h}{{m{v_{1c}}}}$
Substituting the value of ${v_{1c}}$ in above relation,
$
  {\lambda _{1c}} = \dfrac{h}{{m\left( {\dfrac{{{v_1}\vec i - {v_2}\vec j}}{2}} \right)}} \\
  {\lambda _{1c}} = \dfrac{{2h}}{{m\left( {{v_1}\vec i - {v_2}\vec j} \right)}} \\
 $
Converting vector form into normal form, we get
$
  {\lambda _{1c}} = \dfrac{{2h}}{{m\sqrt {\left( {{v_1}^2 + {v_2}^2} \right)} }}\;..................................\left( 1 \right) \\
    \\
 $
By de Broglie wavelength,
${\lambda _1} = \dfrac{h}{{m{v_1}}}$
By rearranging the terms, we get
${v_1} = \dfrac{h}{{m{\lambda _1}}}$
And
${\lambda _2} = \dfrac{h}{{m{v_2}}}$
By rearranging the terms, we get

${v_2} = \dfrac{h}{{m{\lambda _2}}}$
By substituting the values of ${v_1}$ and ${v_2}$ in equation (1), we get
${\lambda _{1c}} = \dfrac{{2h}}{{m\sqrt {\left( {{{\left( {\dfrac{h}{{m{\lambda _1}}}} \right)}^2} + {{\left( {\dfrac{h}{{m{\lambda _2}}}} \right)}^2}} \right)} }}\;$
By taking out the terms $h$ and $m$, by cancelling the square with square root, we get
${\lambda _{1c}} = \dfrac{{2h}}{{\dfrac{{mh}}{m}\sqrt {\left( {\dfrac{1}{{{\lambda _1}^2}} + \dfrac{1}{{{\lambda _2}^2}}} \right)} }}$
By cancelling the common terms in fraction in denominator of RHS,
${\lambda _{1c}} = \dfrac{2}{{\sqrt {\left( {\dfrac{{{\lambda _1}^2 + {\lambda _2}^2}}{{{\lambda _1}{\lambda _2}}}} \right)} }}$
\[{\lambda _{1c}} = \dfrac{{2{\lambda _1}{\lambda _2}}}{{\sqrt {{\lambda _1}^2 + {\lambda _2}^2} }}\]
Similarly, for the de Broglie wavelength of the second particle with respect to the centre of the mass is given by,
\[{\lambda _{2c}} = \dfrac{{2{\lambda _1}{\lambda _2}}}{{\sqrt {{\lambda _1}^2 + {\lambda _2}^2} }}\]

Hence, the option (B) is correct.

Note:
The same steps are followed to find out the de Broglie wavelength of the second particle with respect to the centre of mass which is resulted in the same value which is equal to that of the first particle. Hence, the two particles exhibit the same be Broglie wavelength with respect to the centre of the mass even if they are moving at a right angle to each other.