Question

Two identical long conducting wires AOB and COD are placed at right angles to each other, with one above the other such that ‘O’ is their common point for the two. The wires carry ${I_1}$ and ${I_2}$ currents, respectively. Point I is lying at distance d from O along a direction perpendicular to the plane containing wires. The magnetic field at the point P will be.
A. $\dfrac{{{\mu _0}}}{{2\pi d}}\left( {\dfrac{{{I_1}}}{{{I_2}}}} \right)$
B. $\dfrac{{{\mu _0}}}{{2\pi d}}\left( {{I_1} + {I_2}} \right)$
C. $\dfrac{{{\mu _0}}}{{2\pi d}}\left( {I_1^2 - I_2^2} \right)$
D. $\dfrac{{{\mu _0}}}{{2\pi d}}{\left( {I_1^2 + I_2^2} \right)^{\dfrac{1}{2}}}$

Answer 1

Hint: In order to solve this question, we will use the concept that a wire carrying electric current always produces a magnetic field with closed field lines surrounding the wire. We will calculate the magnetic field at distance d from the both wires and then find the resultant of the magnetic field to reach our answer.

Formula Used- The Biot-Savart Law can be used to determine the magnetic field strength from a current segment. For the simple case of an infinite straight current-carrying wire it is reduced to the form
\[B = \dfrac{{{\mu _0}I}}{{2\pi r}}\]
Where B is the magnetic field due to coil
I is the current, a is the radius of the coil
r is the shortest distance to the wire.

Complete step-by-step answer:
As we know a current carrying wire always produces a magnetic field around it with closed field lines surrounding the wire.
In the given question there will be two magnetic fields due to two wires carrying current ${I_1}$ and ${I_2}$ respectively, which will be perpendicular to each other .

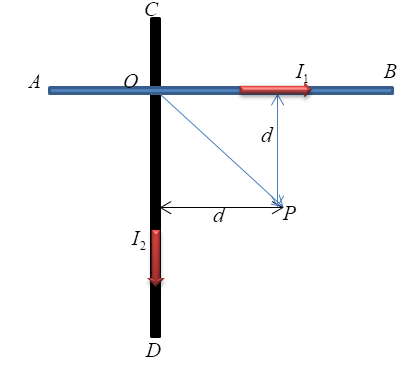
Thus net magnetic fields can be calculated by simple vector sum.
From the formula above, the magnetic field due to wire 1 is given by
${B_1} = \dfrac{{{\mu _0}{I_1}}}{{2\pi d}}$
Also, the magnetic field due to wire 2 is given by
${B_2} = \dfrac{{{\mu _0}{I_2}}}{{2\pi d}}$
The net magnetic field is the vector sum of the two magnetic fields, since both are perpendicular to each other, therefore
$
  {B_{net}} = \sqrt {B_1^2 + B_2^2} \\
  {B_{net}} = \sqrt {{{\left( {\dfrac{{{\mu _0}{I_1}}}{{2\pi d}}} \right)}^2} + {{\left( {\dfrac{{{\mu _0}{I_2}}}{{2\pi d}}} \right)}^2}} \\
  {B_{net}} = \dfrac{{{\mu _0}}}{{2\pi d}}\sqrt {I_1^2 + I_2^2} \\
$
Hence, the net magnetic field is equal to $\dfrac{{{\mu _0}}}{{2\pi d}}\sqrt {I_1^2 + I_2^2} $
Therefore, the correct option is D.

Note: In order to solve these types of problems, remember the Biot- savart law and all the cases related to it like infinite wire, circular coil and many more. The right hand rule is used to determine the direction of the magnetic field from a current; point the thumb in the direction of the current, and the fingers curl in the direction of the magnetic field loops which it creates.