Question

Two identical bar magnets, each having magnetic moment\[M\], are kept at a distance of $2d$ with their axes perpendicular to each other in a horizontal plane. Find the magnetic induction midway between them.
A. $(\sqrt 2 )$$\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{M}{{{d^3}}}$
B. $(\sqrt 3 )$$\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{M}{{{d^3}}}$
C. $\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{M}{{{d^3}}}$
D. $(\sqrt 5 )$$\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{M}{{{d^3}}}$

Answer 1

Hint: As, Bar magnets consist of North pole(N) and South pole(S) and the direction of magnetic induction is always from N to S. We will find magnetic induction due to both bar magnets at mid-point of their axes and will add them using vector algebra.

Formula used:
Since, $B_1$ due to first bar magnet produce magnetic induction in its axial line hence,
$B_1 = \dfrac{{{\mu _0}}}{{4\pi }} \times \dfrac{{2M}}{{{d^3}}}$
Where, $M$ is the magnetic moment of each given bar magnet and ${\mu _0}$ is the vacuum permeability.

Complete step by step answer:
Let us first draw the diagram, consider two bar magnets having both magnetic moments $M$ lying perpendicular to each other at a distance of $2d$ . We will measure this distance from mid-point of the axial bar magnet to the equatorial bar magnet.

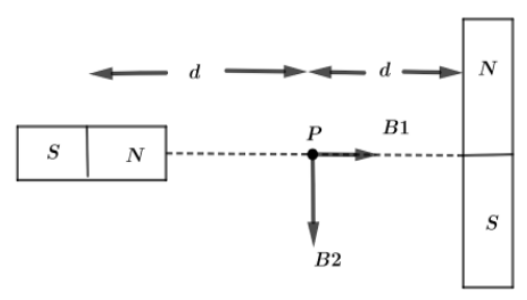
Here, $P$ is the midpoint of two bars lying perpendicular to each other and At this point, $B_1$ is the magnetic induction due to the first bar magnet in the given direction and $B_2$ is the magnetic induction due to the second bar magnet. Since $B_1$ and $B_2$ are perpendicular to each other so net magnetic induction at point $P$ can be calculated as
\[{B_p} = \sqrt {{{(B1)}^2} + {{(B2)}^2}} \].........{Vector addition formula for two perpendicular vectors}
Since, $B1$ due to first bar magnet produce magnetic induction in its axial line hence,
$B_1 = \dfrac{{{\mu _0}}}{{4\pi }} \times \dfrac{{2M}}{{{d^3}}}$
$B_2$ Is the magnetic induction due to the second bar on its equatorial line which is given by?
$B_1 = \dfrac{{{\mu _0}}}{{4\pi }} \times \dfrac{M}{{{d^3}}}$.
Now, net magnetic induction ${B_p}$ is given by
${B_p} = \dfrac{{{\mu _0}}}{{4\pi }} \times \dfrac{M}{{{d^3}}}\sqrt {{2^2} + {1^2}} $
$\therefore {B_p} = \sqrt 5 $$\dfrac{{{\mu _0}}}{{4\pi }} \times \dfrac{M}{{{d^3}}}$.

Hence, correct option is D.

Note:Remember, Magnetic field lines always originate from North Pole (N) and enters to South Pole (S) which shows the direction of magnetic field from N to S but it’s important to note that inside the bar magnet the direction of magnetic induction is always from South Pole (S) to North Pole (N).