Question

Two given straight lines meet in $O$, and through a given point $P$ is drawn a straight line to meet them in $Q$ and $R$; if the parallelogram OQSR be completed find the equation to the locus of $S$.\[\]

Answer 1

Hint: We use the oblique coordinate system with $OQ$ lying on $x-$axis and $OR$ lying on $y-$axis. We assume that the line passing through the fixed point $P$ makes an intercept of length $a$ at $Q$ and an intercept of length $b$ at $R$ when it cuts $y-$axis makes to find the equation of line as $\dfrac{x}{a}+\dfrac{y}{b}=1$. We assume the coordinate of $P\left( h,k \right)$ and the coordinate of $S\left( {{x}_{1}},{{y}_{1}} \right)$. We use the equal sides of parallelogram to find the locus of $S$.

Complete step-by-step solution:
We know that in oblique coordinate systems the coordinate axes are inclined at any angle $ \omega < \ pi $ with horizontal axis $x-$axis. We also know that if any straight line that makes the intercept $a$ with $x-$axis and intercept $b$ with $y-$axis by intersecting them then the equation of straight line in oblique coordinate system in intercept-form is given by
\[ \dfrac{x}{a}+\dfrac{y}{b}=1......\left( 1 \right) \]
We are given in the question that two given straight lines meet in $O$, and through a given point $P$ is drawn a straight line to meet them in $Q$ and $R$. Let us assume that the axes are coordinate axes of oblique coordinate systems with $x-$axis as horizontal axes. The point $P$ is given which means it is a fixed point. Let us assume that the line passing through the fixed point $P$ makes an intercept of length $a$ at $Q$ when it cuts $x-$axis and makes an intercept of length $b$ at $R$ when it cuts $y-$axis. So we have,
\[OQ=a,OR=b\]
 So the equation of the line passing through $P$ is the same as equation (1) that is
\[ \dfrac{x}{a}+\dfrac{y}{b}=1\]
If we denote the coordinates of the fixed point P as $P\left( h,k \right)$ then it will satisfy the above equation. So we have
\[\dfrac{h}{a}+\dfrac{k}{b}=1......\left( 2 \right)\]
We are further given the question that there is a point $S$ which we join with $Q, R$ to get the parallelogram $OQSR$. We are asked to find the locus of $S$. The rough figure is drawn below. \[\]

 

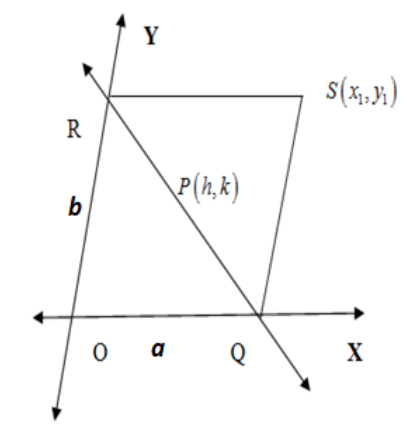
Let at one instant the coordinate of $S$ be $S\left( {{x}_{1}},{{y}_{1}} \right)$. So we have equal opposite sides in parallelogram. So we have,
\[\begin{align}
  & OQ=QS\Rightarrow a={{x}_{1}} \\
 & OR=RQ\Rightarrow b={{y}_{1}} \\
\end{align}\]
We put the above obtained values in equation (2) to have
$\dfrac{h}{{{x}_{1}}}+\dfrac{k}{{{y}_{1}}}=1......\left( 3 \right)$
We now take substitute variable point $S\left( x,y \right)$ in above equation for all instances during movement of $S$ in place of $S\left( {{x}_{1}},{{y}_{1}} \right)$ and find locus of $S$ as,
\[\dfrac{h}{x}+\dfrac{k}{y}=1\]

Note: We note that the equation of line inclined at an angle $\theta $ with $x-$axis where axes are inclined at an angle $\omega $ in oblique coordinate system is given by $y=mx+c$ where $\tan \theta =\dfrac{m\sin \omega }{1+\cos \omega }$ and $m$ is the slope in rectangular coordinate system. The equation in intercept form $\dfrac{x}{a}+\dfrac{y}{b}=1$ is the same in the oblique, rectangular and polar coordinate system.