Question

Two fixed charges A and B of $ 5\mu C $ each are separated by a distance of 6 m. C is the mid point of the line joining A and B. A charge 'Q' of $ -5\mu C $ is shot perpendicular to the line joining A and B through C with a kinetic energy of 0.06 J. The charge 'Q' comes to rest at a point D. The distance CD is :
 $ \begin{align}
 & \text{A}\text{. 3m} \\
 & \text{B}\text{. }\sqrt{3}\text{m} \\
 & \text{C}\text{. 3}\sqrt{3}\text{m} \\
 & \text{D}\text{. 4m} \\
\end{align} $

Answer 1

Hint: First try to draw the diagram as given in the question, Now try to find the initial potential energy in the system. After we get the initial potential energy, we have to find the total initial energy of the system. Now, apply the law of conservation of energy and find the magnitude of one side of the triangle formed. From that side apply the Pythagoras theorem to get the required value.

Formula used:
$ U=K\left( \dfrac{{{Q}_{1}}{{Q}_{2}}}{{{r}_{12}}}+\dfrac{{{Q}_{2}}{{Q}_{3}}}{{{r}_{23}}}+\dfrac{{{Q}_{3}}{{Q}_{1}}}{{{r}_{13}}} \right) $
E = U + K . E
\[\text{hypotenus}{{\text{e}}^{2}}=\text{ perpendicula}{{\text{r}}^{2}}\text{ + bas}{{\text{e}}^{2}}\]

Complete step-by-step answer:

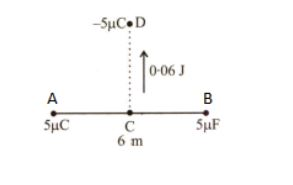
Here in the above diagram we see that, at two points A and B we see a charge of $ 5\mu C $ , and the distance between the two charges are 6 m, now at point D a charge of $ -5\mu C $ , is shot just perpendicular to the midpoint of charge AB with a kinetic energy of 0.06 J.
Now according to the problem,
Initial potential energy of the system must be,
 $ U=K\left( \dfrac{{{Q}_{1}}{{Q}_{2}}}{{{r}_{12}}}+\dfrac{{{Q}_{2}}{{Q}_{3}}}{{{r}_{23}}}+\dfrac{{{Q}_{3}}{{Q}_{1}}}{{{r}_{13}}} \right) $ , K=constant. $ U=9\times {{10}^{9}}\left( \dfrac{5\times {{10}^{-6}}\times 5\times {{10}^{-6}}}{6}+\dfrac{5\times {{10}^{-6}}\times -5\times {{10}^{-6}}}{3}+\dfrac{5\times {{10}^{-6}}\times -5\times {{10}^{-6}}}{3} \right) $ , now substituting the values with,
 (K= $ 9\times {{10}^{9}} $ , $ {{Q}_{1}}=5\times {{10}^{-6}} $ , $ {{Q}_{2}}=5\times {{10}^{-6}} $ , $ {{Q}_{3}}=-5\times {{10}^{-6}} $ ),
On solving this we get the initial potential energy as, U= -0.1125 J
Therefore we know that the system already has a kinetic energy of 0.06J, so the total initial energy of the system is,
E = U + K . E,
E = -0.1125 + 0.06 = -0.0525 J.
Now, at D, the charge $ -5\mu C $ comes to rest, so we can say that the total energy is equal to the potential energy at that point.
Now if we extend two lines from ‘A’ and ‘B’ to point D.

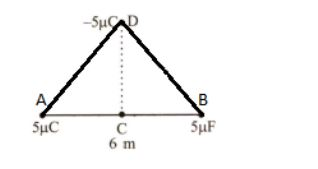
Now by using symmetry, we can say that AD=BD.
On, applying law of conservation of energy,
 $ -0.0525=9\times {{10}^{9}}\left( \dfrac{5\times {{10}^{-6}}\times 5\times {{10}^{-6}}}{6}+\dfrac{5\times {{10}^{-6}}\times -5\times {{10}^{-6}}}{AD}+\dfrac{5\times {{10}^{-6}}\times -5\times {{10}^{-6}}}{BD} \right) $ ,
Therefore on solving the above equation, we get AD=5m
 If we apply Pythagoras theorem, we get
 $ \text{A}{{\text{D}}^{2}}\text{=A}{{\text{C}}^{2}}\text{+C}{{\text{D}}^{2}} $
 $ {{\text{5}}^{2}}\text{=}{{\text{3}}^{2}}\text{+C}{{\text{D}}^{2}} $
CD= 4 m

So, the correct answer is “Option D”.

Note: In the formula for initial potential energy, k is the proportionality constant known as coulomb’s law constant, this value totally depends on the medium in which the charged objects are placed. Pythagoras theorem states that,
\[\text{hypotenus}{{\text{e}}^{2}}=\text{ perpendicula}{{\text{r}}^{2}}\text{ + bas}{{\text{e}}^{2}}\] .