Question

Two equal resistance when connected in series to a battery, consumes electric power of $60W$. If these resistances are now connected in parallel combination to the same battery, the electric power consumed will be.
A) $60W$
B) $240W$
C) $30W$
D)$120W$

Answer 1

Hint: Power is defined as the rate of doing work. We must remember that in series combination the equivalent resistance is different than in parallel combination. So power in both will be different.

Formula used:
Power $(P) = VI = {I^2}R = \dfrac{{{V^2}}}{R}$, where $V$ is potential difference , $R$ is resistance and $I$ is current flowing through the resistance.

Complete step by step answer:We have given that initially two equal resistance are connected in series combination to a battery as shown in the figure.

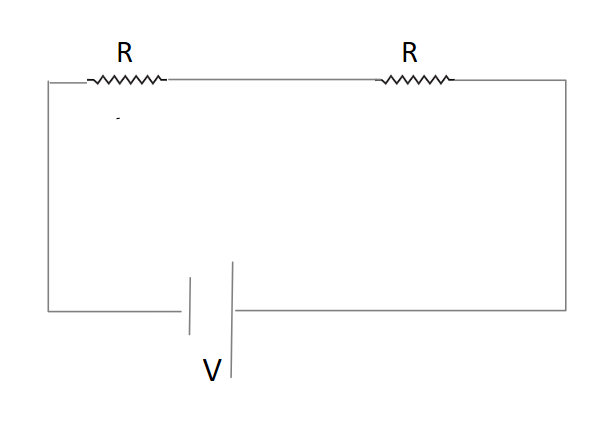
Let us assume that Resistance of both is $R$. So equivalent resistance in this case will be ${R_{eq}} = R + R = 2R$ because in series combination resistances are directly added.
Also assume that Voltage of battery is $V$.
So according to the formula as written above, power generated in this case will be
$P = \dfrac{{{V^2}}}{{{R_{eq}}}} = \dfrac{{{V^2}}}{{2R}}$ and in question we have given this value as $60W$.
So we can say that $\dfrac{{{V^2}}}{{2R}} = 60W$ and we can also write $\dfrac{{{V^2}}}{R} = 120W$--(1)
Now both resistances are connected in parallel combination as shown in the figure.

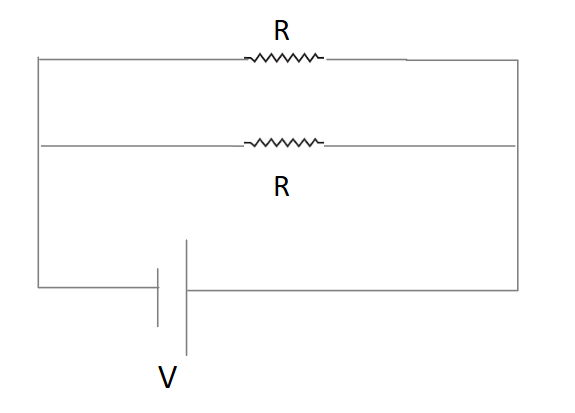
As we know that equivalent resistance in parallel combination is calculated as
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
We have given that both resistances are same, so Equivalent resistance in this case will be
$
  \dfrac{1}{{{R_{eq}}}} = \dfrac{2}{R} \\
   \Rightarrow {R_{eq}} = \dfrac{R}{2} \\
 $
As the battery is same so Voltage of battery will not be changing here.
We can write Power generated in this case will be ${P_2}$
$
  {P_2} = \dfrac{{{V^2}}}{{{R_{eq}}}} = \dfrac{{{V^2}}}{{R/2}} \\
  \Rightarrow {P_2} = \dfrac{{2{V^2}}}{R} \\
 $
From equation 1, we can substitute the value of $\dfrac{{{V^2}}}{R} = 120W$
So we can get the value of Power in this case as
$P = 240W$

Therefore, option B is correct.

Note:There are 3 formulas to calculate power in current Electricity. Which are
1) $P = VI$
2) $P = {I^2}R$
3) $P = \dfrac{{{V^2}}}{R}$
Students can be confused about which formula he or she should use. You can use any formula. It will give you the same results but if we are using the second or first formula where we need the value of current, it would be a bit lengthy process for us. So remember and take care to use that formula for which you already have values like in this question we know battery is same so Voltage will be same in both cases and Equivalent resistance we have calculated according to Combination so we used Third Formula i.e $P = \dfrac{{{V^2}}}{R}$.