Question

Two equal and negative charges $ - q $ are fixed at point $ (0,a) $ and $ (0, - a) $ on the $ Y $ -axis. A positive charge $ Q $ is related from rest at a point $ (2a,0) $ on the $ X $ -axis. What will be the type of motion that charge $ Q $ will exhibit?
(A) Execute simple harmonic motion
(B) Move to the origin and remain at rest there
(C) move to infinity
(D) Execute oscillatory but not simple harmonic motion

Answer 1

Hint :Find the net coulomb’s force on the charge $ Q $ and deduce the relation between the displacement from origin and the coulomb’s force.The coulomb’s force, $ \overrightarrow {{F_x}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Qq}}{{{x^2}}}{\kern 1pt} \widehat x $ Where, $ Q $ is a charge separated by distance $ x $ from another charge $ q $ then Force on each charge by the other charge is $ {F_x} $ , $ {\varepsilon _0} $ is the permittivity of vacuum or air.
For oscillatory motion, Force is $ F\alpha - x{(t)^n} $ where, $ n $ is any integer. $ x(t) $ is the displacement of the particle at any point of time.

Complete Step By Step Answer:
At first we need to find the coulomb’s force on the charge $ Q $ due to the other two charges using the formula, $ \overrightarrow {{F_x}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{Qq}}{{{x^2}}}{\kern 1pt} \widehat x $ Where, $ Q $ is a charge separated by distance $ x $ from another charge $ q $ then Force on each charge by the other charge is $ {F_x} $ , $ {\varepsilon _0} $ is the permittivity of vacuum or air.

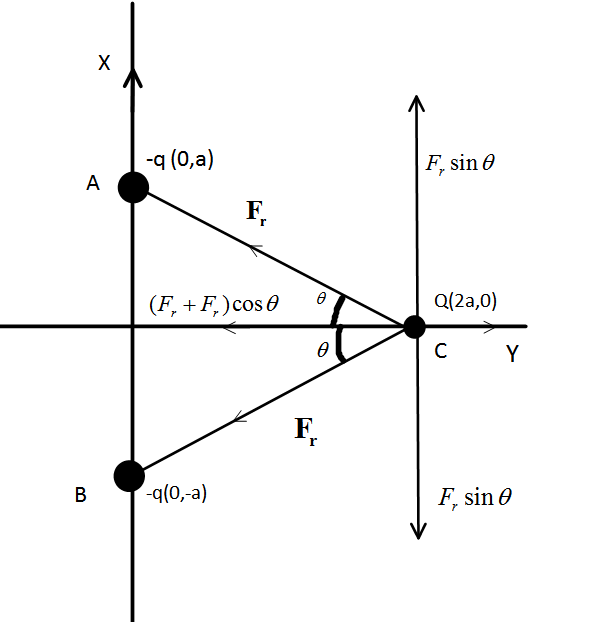
Here, in the diagram you can see that the one charge $ - q $ is placed at $ (0,a) $ and another charge is placed at $ (0, - a) $ .The charge $ Q $ is placed at $ (2a,0) $ . So, force on charge $ Q $ by both the charges at A and B will be,
 $ \overrightarrow {{F_{2r}}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - Qq}}{{{r^2}}}\widehat {AC} $ and $ \overrightarrow {{F_{1x}}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - Qq}}{{{r^2}}}\widehat {BC} $ where, $ {r^2} = {x^2} + {a^2} $ $ \overrightarrow {{F_{1r}}} $ and $ \overrightarrow {{F_{2r}}} $ are forces by the charge at $ (0,a) $ and $ (0, - a) $ on $ Q $ respectively and $ \widehat {AB} $ and $ \widehat {BC} $ are the unit vectors towards the charge at $ (0,a) $ and $ (0, - a) $ respectively when the distance varies, say the distance be $ r $ that means the charge is at $ (r,0) $ .
Hence, $ \overrightarrow {{F_{2r}}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - Qq}}{{{{(\sqrt {{x^2} + {a^2}} )}^2}}}\widehat {AC} $ and $ \overrightarrow {{F_{1r}}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - Qq}}{{{{(\sqrt {{x^2} + {a^2}} )}^2}}}\widehat {BC} $ .
Now, we can see that both the forces are equal in magnitude i.e. $ \left. {\left| {\overrightarrow {{F_{1r}}} } \right.} \right| = \left. {\left| {\overrightarrow {{F_{2r}}} } \right.} \right| = {F_r} $ Now, the force is attractive since it has a negative sign.
Now, the component of the forces according to the figure is $ {F_r}\cos \theta $ towards $ - X $ axis for both the charges at $ (0,a) $ and $ (0, - a) $ , and along $ Y $ axis it is $ {F_r}\sin \theta $ along $ - Y $ for the charge at $ (0,a) $ and along $ Y $ due to the charge at $ (0, - a) $ . where, $ \theta $ is the angle between the $ X $ axis and the line of force that means angle between $ AC $ and $ BC $ . Both the $ - q $ charges are at the same distance from origin hence $ \theta $ is the same for both of them.
Therefore, these two forces cancel out each other since they are equal in magnitude but opposite in direction i.e. $ \left. {\left| {\overrightarrow {{F_{1r}}} } \right.} \right|sin\theta = \left. {\left| {\overrightarrow {{F_{2r}}} } \right.} \right|sin\theta = {F_r}sin\theta $
Therefore, the total force on $ Q $ is acting towards $ - X $ direction and magnitude of it is $ {F_r}\cos \theta + {F_r}\cos \theta $
That becomes,
  $ = 2{F_r}\cos \theta $
Now, $ \cos \theta = \dfrac{x}{{\sqrt {{x^2} + {a^2}} }} $
Therefore, the force becomes
 $ 2{F_r}\cos \theta = 2 \cdot \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - Qq}}{{{{(\sqrt {{x^2} + {a^2}} )}^2}}} \cdot \dfrac{x}{{\sqrt {{x^2} + {a^2}} }} $
 $ = 2 \cdot \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - Qqx}}{{{{({x^2} + {a^2})}^{\dfrac{3}{2}}}}} $
Now, for $ x = 2a $ you can see that that,
 $ {F_R} = 2{F_r}\cos \theta = 2 \cdot \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - Qq2a}}{{{{(4{a^2} + {a^2})}^{\dfrac{3}{2}}}}} $
 $ = 2 \cdot \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - Qq2a}}{{{{(5{a^2})}^{\dfrac{3}{2}}}}} $
On simplifying we get
 $ = 2 \cdot \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - Qq2a}}{{{{(5a)}^3}}} $
 $ = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - Qqa}}{{5\sqrt 5 {a^3}}} $
 $ = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - Qq}}{{5\sqrt 5 {a^2}}} $
That means,
 $ {F_R}\alpha - {a^{ - 2}} $ at start which is an equation of oscillatory motion but not harmonic. After the motion starts the position changes and also the force then the force acting on the charge is as before when the charge was at $ r $ and that force is $ {F_R} = 2 \cdot \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - Qqx}}{{{{({x^2} + {a^2})}^{\dfrac{3}{2}}}}} $ which is $ \alpha - {x^{ - 2}} $ which is again oscillatory but not harmonic. Since, for simple harmonic motion force is proportional to displacement i.e. $ F\alpha - x(t) $ where $ x(t) $ is displacement of the particle at any point of time
But for oscillatory motion it is $ F\alpha - x{(t)^n} $ where $ n $ is any integer.

Note :
 $ \bullet $ Components of forces need to be calculated with respect to the angle between the line of force and any of the axes properly.
 $ \bullet $ Sine component would not have canceled out if the charges were unequal.
 $ \bullet $ Simple harmonic is the simplest type of oscillatory motion.