Question

Two crossroads, each 2 m wide, run at right angles through the center of a rectangular park of length 64 m and breadth 38 m, such that each is parallel to one of the sides of the rectangle. Find the area of the roads. Also, find the area of the remaining part of the park.

Answer 1

Hint: Since it is mentioned that the park is rectangular in shape, so find the area of the using the formula $\left( l\times b \right)$ where l is length and b is the breadth of the park. Also, we have two roads that run parallel to each side of the rectangle, so the length of one of the roads is equal to the length of the park, and the breadth of the other roads is equal to the breadth of the park. Since the roads are also in a rectangular shape, find their area using the same formula $\left( l\times b \right)$. To find the remaining area, subtract the area of roads as well as the common area of the roads from the area of the rectangle.

Complete step-by-step answer:
The figure below shows the rectangular park where ${{R}_{1}}$ and ${{R}_{2}}$ are two roads running parallel to the sides of the park.

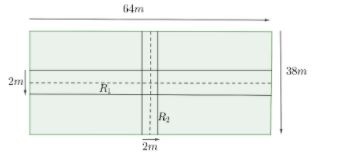
Since we have a rectangular park, whose length is 64 m and breadth is 38 m.
So, the area of the park is:
$\begin{align}
  & A=l\times b \\
 & =64\times 38 \\
 & =2432\text{ }{{m}^{2}}......(1)
\end{align}$
Since the roads are running parallel to the sides of the park as shown in the figure.
So, the length of the road ${{R}_{1}}$ is 64 m and the breadth of ${{R}_{1}}$ is 2 m.
Similarly, the length of ${{R}_{2}}$ is 2 m and the breadth of ${{R}_{2}}$ is 38 m.
So, by using the formula $\left( l\times b \right)$, we get the areas of both roads as:
Area of ${{R}_{1}}$
 $\begin{align}
  & =64\times 2 \\
 & =128\text{ }{{m}^{2}}......(2) \\
\end{align}$
Area of ${{R}_{2}}$
$\begin{align}
  & =2\times 38 \\
 & =76\text{ }{{m}^{2}}......(3) \\
\end{align}$
Now, find the common area of roads, i.e. a square with side 2m
So, we get:
$\begin{align}
  & A=2\times 2 \\
 & =4{{m}^{2}}......(4)
\end{align}$
Now, we need to find the area of the remaining part of the rectangular park.
i.e. Area of park – sum of area of roads – area of the common region of the roads
Therefore, area of remaining part of park is:
$\begin{align}
  & =2432-\left( 128+76+4 \right) \\
 & =2224\text{ }{{m}^{2}} \\
\end{align}$

Note: Since it is mentioned that the roads are at right angles to each other, so we have a number of possible situations in which roads might be running through the park. But it is also said that they are running through the center of the park, so the figure shown above is the only possible situation that can be drawn from the question.