Question

Two copper wires x and y have the same volume. Wire y is four times as long as wire x. Find the ratio of resistance of wire y to that of wire x.

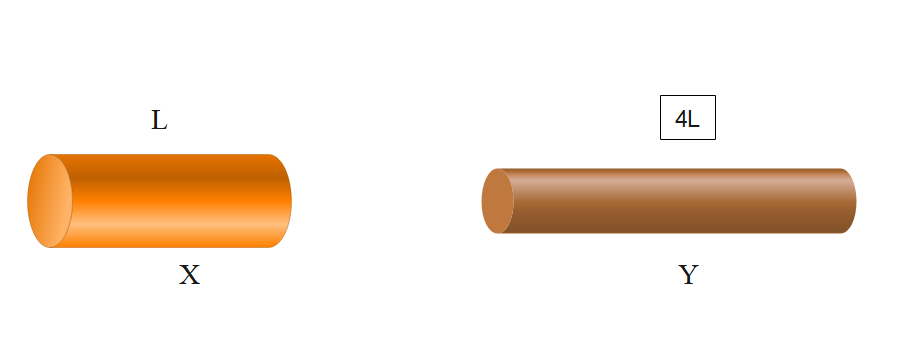
$\begin{align}
  & a)1 \\
 & b)4 \\
 & c)8 \\
 & d)16 \\
\end{align}$

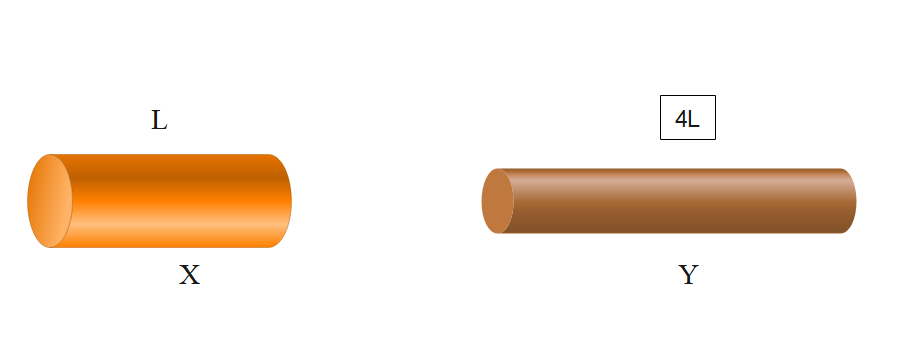
Answer 1

Hint: Find the ratio between the areas of the two copper wires as length is given and we know the volumes of both wires are equal. Resistance depends on the resistivity, area and length of the wires. As we know, all the terms, we can find the ratio easily.
Formula used:
$\begin{align}
  & V=A\times l \\
 & R=\dfrac{\rho l}{A} \\
\end{align}$

Complete answer:
Let us first find the relation between the areas of the two copper wires. We know, the volumes of both the copper wires is same and the relation between length is given,
Now,
$\begin{align}
  & V=A\times l \\
 & \Rightarrow {{A}_{x}}\times {{l}_{x}}={{A}_{y}}\times {{l}_{y}} \\
 & \Rightarrow {{A}_{x}}\times L={{A}_{y}}\times 4L \\
 & \Rightarrow \dfrac{{{A}_{x}}}{{{A}_{y}}}=4 \\
\end{align}$
Now, we know the relation between the areas of the copper wires, length of the copper wires. The resistivity for two copper wires is same because the two wires are made of same material.
Therefore,
$\begin{align}
  & R=\dfrac{\rho l}{A} \\
 & \Rightarrow {{R}_{1}}=\dfrac{\rho L}{{{A}_{x}}} \\
 & \Rightarrow {{R}_{2}}=\dfrac{\rho \times 4L}{{{A}_{y}}} \\
 & \Rightarrow \dfrac{{{R}_{1}}}{{{R}_{2}}}=\dfrac{\dfrac{\rho L}{{{A}_{x}}}}{\dfrac{\rho \times 4L}{{{A}_{y}}}} \\
 & \Rightarrow \dfrac{{{R}_{1}}}{{{R}_{2}}}=\dfrac{{{A}_{y}}}{4\times {{A}_{x}}} \\
 & \Rightarrow \dfrac{{{R}_{1}}}{{{R}_{2}}}=\dfrac{1}{16} \\
 & \Rightarrow \dfrac{{{R}_{2}}}{{{R}_{1}}}=16 \\
\end{align}$

So, the correct answer is “Option D.

Additional Information:
Resistivity is the measure of resistance of a given size of specific material to electrical conduction. It is sometimes referred to as the specific electrical resistance or volume resistivity. These terms aren’t used widely nowadays. Resistance is the property of a conductor to resist or oppose the flow of electric current through the conductor. Resistivity units are si system of measurement is siemens per meter. The resistivity of any material depends on the area of the material, area of the conductor and the resistance of the conductor or material. Resistivity is denoted by the Greek letter rho.

Note:
There's a difference between the formula of resistance and resistivity. Many of us confuse that resistance is resistivity times the area per length. But it is the opposite, the resistance is the resistivity times the length per area. The units of resistance are ohms and that of resistivity is ohm meter.