Question

Two copper wires A and B having lengths in the ratio of $2:1$, area of cross section in the ratio of $1:2$ are connected to a battery of potential difference $v$ separately. Find the ratio of current density A to B.

Answer 1

Hint: The ohm’s law is used in order to solve this question. The current is obtained by taking the ratio of the voltage and the resistance of the wires. The resistivity is also obtained from the equation of resistance. The current density is the product of the current passing and the area of the cross section.

Complete step-by-step answer:

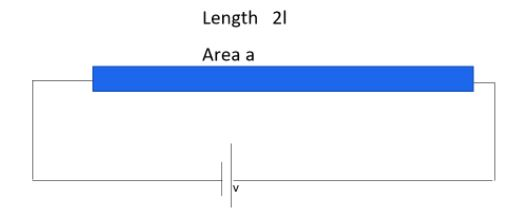
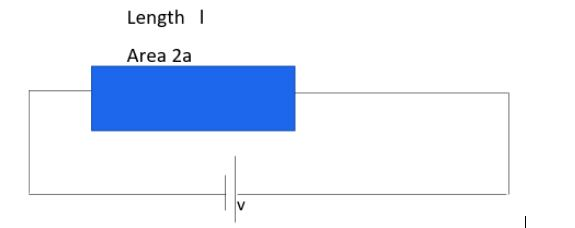
It has been give the ratio of the length of the copper wires as,
${{l}_{a}}:{{l}_{b}}=2:1$
The ratio of the area of the cross section of the wire is also mentioned in the question as,
${{A}_{a}}:{{A}_{b}}=1:2$
According to ohm’s law we can write that the voltage in a wire is given as the product of the current passing through it and the resistance of the wire.
This can be written as an equation as,
$V=IR$
From this the value of the current is given as,
\[I=\dfrac{V}{R}\]……… (1)
As we all know, the resistance is given by the equation,
\[R=\dfrac{\rho l}{A}\]
Where \[\rho \] be the resistivity of the wire which is a constant.
Now put the value of the resistance in the equation (1)
\[I=\dfrac{V}{\left( \dfrac{\rho l}{A} \right)}=\dfrac{VA}{\rho l}\]
Comparing the conditions in both the wires can be shown as,
\[\dfrac{{{I}_{a}}}{{{I}_{b}}}=\dfrac{V{{A}_{a}}}{\rho {{l}_{a}}}\times \dfrac{\rho {{l}_{b}}}{V{{A}_{b}}}\]
Simplifying the equation by cancelling the common terms will be written as,
\[\dfrac{{{I}_{a}}}{{{I}_{b}}}=\dfrac{{{A}_{a}}}{{{l}_{a}}}\times \dfrac{{{l}_{b}}}{{{A}_{b}}}\]
Rearranging this equation will be written as,
\[\dfrac{{{I}_{a}}}{{{I}_{b}}}=\dfrac{{{A}_{a}}}{{{A}_{b}}}\times \dfrac{{{l}_{b}}}{{{l}_{a}}}\]
The current density is found by the equation,
\[J=IA\]
Comparing the current densities of both the wires will be,
\[\dfrac{{{J}_{a}}}{{{J}_{b}}}=\dfrac{{{I}_{a}}{{A}_{b}}}{{{I}_{b}}{{A}_{a}}}\]
Substituting the values of the currents in it will give,
$\dfrac{{{J}_{a}}}{{{J}_{b}}}=\dfrac{{{A}_{a}}{{l}_{b}}{{A}_{b}}}{{{A}_{b}}{{l}_{a}}{{A}_{a}}}=\dfrac{{{l}_{b}}}{{{l}_{a}}}$
Substituting the length ratio in it will give,
\[\dfrac{{{J}_{a}}}{{{J}_{b}}}=\dfrac{{{l}_{b}}}{{{l}_{a}}}=\dfrac{1}{2}\]
Therefore the answer for the question is calculated.

Note: Current density is defined as the quantity of charge per unit time which will flow through a unit area of a given cross section of the material. The unit of this quantity is expressed in amperes per square metre. The current density is a vector quantity also.