Question

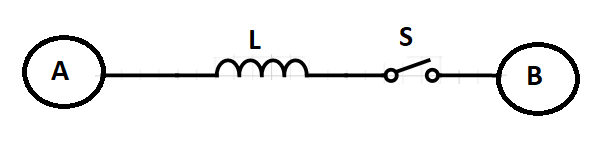
Two conducting spheres of radius $R$ are placed at a large distance from each other. They are connected by a coil of inductance $L$, as shown in the figure. Sphere A is given a charge of $Q$ and the switch ‘S’ is closed at time $t = 0$. Find charge on sphere B as a function of time. At what time charge on B is $\dfrac{Q}{2}$?

Answer 1

Hint: The spherical capacitor of any conducting solid sphere of radius $R$ is $C = 4\pi {\varepsilon _0}R$. Where ${\varepsilon _0}$ is the permittivity of free space.
The potential on the surface of a conducting sphere is $V = \dfrac{Q}{{4\pi {\varepsilon _0}R}}$. Where $Q$ is the total charge on the surface of the sphere.
Find the potential difference across the inductor. Then you will get a familiar differential equation like $\dfrac{{{d^2}x}}{{d{t^2}}} + ax = 0$. The general solution of this equation is $x = A\cos at + B\sin at$. Now find the values of $A$ and $B$ by the application of the initial condition.

Complete step by step answer:
It is given that the radius of the two conducting spheres A and B is $R$.
The charge on sphere A is $Q$.
The sphere A and B are connected through an inductor of inductance $L$.
Switch S is closed at time $t = 0$
Consider the charge on the sphere B is $Q'$ at a time $t = t$
The charge on the sphere A at the same time $t = t$ is $Q - Q'$
The current through the inductor is $i = \dfrac{{dQ'}}{{dt}}$
The potential on the surface of the sphere A, ${V_A} = \dfrac{{Q - Q'}}{{4\pi {\varepsilon _0}R}}$
The potential on the surface of the sphere B, ${V_B} = \dfrac{{Q'}}{{4\pi {\varepsilon _0}R}}$
Both the spheres have equal spherical capacitance, ${C_A} = {C_B} = 4\pi {\varepsilon _0}R$
Sphere A and B are connected in series, The effective capacitance is $C = \dfrac{{{C_A}}}{2} = 2\pi {\varepsilon _0}R$
Now the e.m.f. induced across the inductor is given by
$E = - L\dfrac{{di}}{{dt}}$
Or ${V_A} - {V_B} = - L\dfrac{{di}}{{dt}}$
Substitute all the required values
$ \Rightarrow \dfrac{{Q - Q'}}{{4\pi {\varepsilon _0}R}} - \dfrac{{Q'}}{{4\pi {\varepsilon _0}R}} = - L\dfrac{{{d^2}Q'}}{{d{t^2}}}$
$ \Rightarrow \dfrac{{Q - 2Q'}}{{4\pi {\varepsilon _0}R}} = - L\dfrac{{{d^2}Q'}}{{d{t^2}}}$
Further simplify to get a differential equation.
$ \Rightarrow \dfrac{{{d^2}Q'}}{{d{t^2}}} + \dfrac{1}{{2\pi {\varepsilon _0}RL}}\left( {\dfrac{Q}{2} - Q'} \right) = 0$
We know that the angular frequency $\omega = \sqrt {\dfrac{1}{{LC}}} $
Or $\omega = \sqrt {\dfrac{1}{{2\pi {\varepsilon _0}RL}}} $
$ \Rightarrow \dfrac{{{d^2}Q'}}{{d{t^2}}} + \omega \left( {\dfrac{Q}{2} - Q'} \right) = 0$
Let $q = \dfrac{Q}{2} - Q'$, Then $\dfrac{{{d^2}q}}{{d{t^2}}} = - \dfrac{{{d^2}Q'}}{{d{t^2}}}$
The above equation becomes
$ \Rightarrow \dfrac{{{d^2}q}}{{d{t^2}}} - \omega q = 0$ …… (1)
The general Solution of the above differential equation is given by
$q = A\cos \omega t - B\sin \omega t$ …… (2)
Now we have to find the values of $A$ and $B$.
At time $t = 0$, $Q' = 0$, So $q = Q$
$Q = A\cos 0 - B\sin 0$
$ \Rightarrow A = Q$
Now $i = \dfrac{{dQ'}}{{dt}} = - \dfrac{{dq}}{{dt}}$
Or $i = - \left( { - A\sin \omega t - B\cos \omega t} \right)$
Or $i = A\sin \omega t + B\cos \omega t$
At time $t = 0$, $i = 0$, We got
$0 = A\sin 0 + B\cos 0$
$ \Rightarrow B = 0$
The equation (2) becomes
$q = Q\cos \omega t$
$ \Rightarrow \dfrac{Q}{2} - Q' = Q\cos \omega t$
$ \Rightarrow Q' = \dfrac{Q}{2}\left( {1 - \cos \omega t} \right)$ …… (3)
Hence, the charge on the surface of the sphere B at a time $t = t$ is $\dfrac{Q}{2}\left( {1 - \cos \omega t} \right)$.
Now we have to find the time when the charge on sphere B is $\dfrac{Q}{2}$.
i.e., From equation (3), $1 - \cos \omega t = 1$
$ \Rightarrow \cos \omega t = 0$
$ \Rightarrow \cos \omega t = \cos \dfrac{\pi }{2}$
Or $\omega t = \dfrac{\pi }{2}$
Now substitute the value $\omega = \sqrt {\dfrac{1}{{2\pi {\varepsilon _0}RL}}} $, We got
$ \Rightarrow t = \dfrac{\pi }{2}\sqrt {2\pi {\varepsilon _0}RL} $
Hence, at the time $t = \dfrac{\pi }{2}\sqrt {2\pi {\varepsilon _0}RL} $, the charge on the surface of the sphere B will be $\dfrac{Q}{2}$.

Note:
The given circuit diagram is a LC oscillations circuit. Where the two conducting spheres act as spherical capacitors. When a charged capacitor is allowed to discharge through an inductor, electrical oscillations are produced. These oscillations are called LC oscillations.
The frequency of oscillating charge is given by $f = \dfrac{1}{{2\pi \sqrt {LC} }}$.