Question

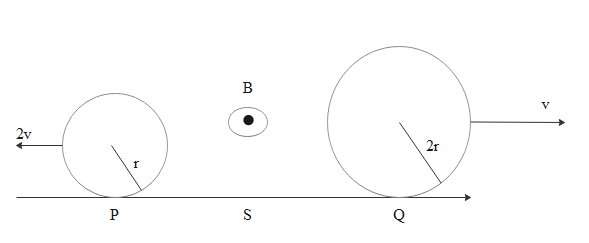
Two conducting rings P and Q of radii and r and 2r rotate uniformly in opposite directions with centre of mass velocities 2 v and v respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicular to the plane of the rings. The potential difference between the highest points of the two rings is

 

A. zero
B. 4 Bvr
C. 8 Bvr
D.16 Bvr

Answer 1

Hint:In electromagnetic induction when a conductor is moving with certain velocity in the presence of magnetic field then voltage will be generated across the conductor and this is called the induced emf. This happens due to change in the flux which is associated with that conductor. This problem is related to the induced emf.

Formula used:
$e = \dfrac{{BVL\sin \theta }}{2}$

Complete answer:
We have a term called the motional emf which is induced by the motion of a body in a constant magnetic field. The emf generated in this case is motional emf and its formula generally is given by $e = BVL\sin \theta $
Here e is the induced motional emf and it is to be noted that the B and V and L should be mutually perpendicular to each other.

In the question it is given that rings are travelling in opposite directions and since those rings are rolling that means they are having pure rotation with respect to the ground contact point. We can assume a rod rotating with respect to the contact points and velocity length of the rod and magnetic field are mutually perpendicular to each other. Hence sinusoidal function in motional emf formula will become one. The formula for motional emf when rod is rotating is $e = \dfrac{{BVL}}{2}$

Where V is the velocity of the tip of the rod, L is the effective length i.e diameter of the ring here and B is the magnetic field. Since both rings are moving in opposite directions polarities of top points will have opposite signs. So in finding difference we can just add the magnitude of emf’s
Top point of the rotation of ring will have twice the linear velocity of ring
Magnitude of emf induced emf in first ring is ${e_1} = \dfrac{{BVL}}{2} = \dfrac{{B \times 4v \times 2r}}{2} = 4Bvr$
For second ring it will be ${e_1} = \dfrac{{BVL}}{2} = \dfrac{{B \times 2v \times 4r}}{2} = 4Bvr$
So the difference would be adding of two emfs as their polarities are opposite so it will be $8Bvr$

So, the correct answer is “Option C”.

Note:
When the rod is rotating we can think like the point of rotation doesn’t have any velocity so it doesn’t have any emf. The tip of the rod has some velocity so it has some emf. Now by doing average of both we got the above result. Otherwise if there is only translation then that 2 will not be there in the formula.