Question

Two concentric thin metallic spheres of radii $ {R_1} $ and $ {R_2} $ $ \left( {{R_1} > {R_2}} \right) $ bear charges $ {Q_1} $ and $ {Q_2} $ respectively. Then the potential at a radius $ r $ between $ {R_1} $ and $ {R_2} $ will be $ 1/4(\pi {\varepsilon _0}) $ times:
(A) $ \dfrac{{{Q_1} + {Q_2}}}{4} $
(B) $ \dfrac{{{Q_1}}}{{{R_1}}} + \dfrac{{{Q_2}}}{r} $
(C) $ \dfrac{{{Q_1}}}{{{R_1}}} + \dfrac{{{Q_2}}}{{{R_2}}} $
(D) $ \dfrac{{{Q_1}}}{{{R_2}}} + \dfrac{{{Q_2}}}{{{R_1}}} $

Answer 1

Hint: We consider two concentric thin metallic spheres of radii $ {R_1} $ containing a charge $ {Q_1} $ and $ {R_2} $ containing a charge $ {Q_2} $ . We are considering a particular radius $ r $ that is located between the radii of the two spheres. We have to find the potential at this particular radius.

Complete Step by step solution:
There will be potential due to the two charged spheres.
The radius $ r $ will be inside the sphere of radius $ {R_1} $ and outside the sphere of radius $ {R_2} $ as shown in the figure.

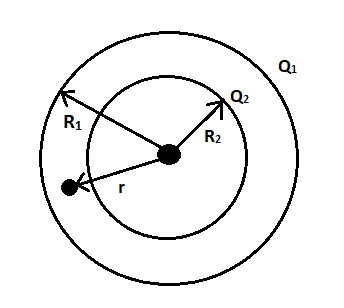
Let the potential due to the sphere of radius $ {R_2} $ be $ {V_2} = k\dfrac{{{Q_2}}}{r} $ since $ r $ is outside the sphere
Let the potential due to the sphere of radius $ {R_1} $ be $ {V_1} = k\dfrac{{{Q_1}}}{{{R_1}}} $ as the radius $ r $ is inside the sphere the potential will be constant.
The total potential at the radius $ r $ can be written as,
 $ {V_r} = {V_1} + {V_2} $
Substituting the values of $ {V_1} $ and $ {V_2} $ within the above equation, we get
 $ {V_r} = k\dfrac{{{Q_2}}}{r} + k\dfrac{{{Q_1}}}{{{R_1}}} $
Taking the common term $ k $ outside, we get
 $ {V_r} = k\left( {\dfrac{{{Q_1}}}{{{R_1}}} + \dfrac{{{Q_2}}}{r}} \right) $
It is given that $ k = 1/4(\pi {\varepsilon _0}) $
The answer is: Option (B): $ \dfrac{{{Q_1}}}{{{R_1}}} + \dfrac{{{Q_2}}}{r} $ .

Additional Information
Surfaces having the same potential at every point is called equipotential surfaces. The electric field is usually normal to the equipotential surface. For moving a charge on the equipotential surface no work is required.

Note:
There is a potential associated with every field. The potential associated with an electric field is called electric potential. It is a scalar quantity. The electric field to some extent is the negative gradient of the electrical potential at that point. It is the work done in bringing a positive charge $ q\; $ from infinity to that point. The potential decreases within the direction of the electrical field.