Question

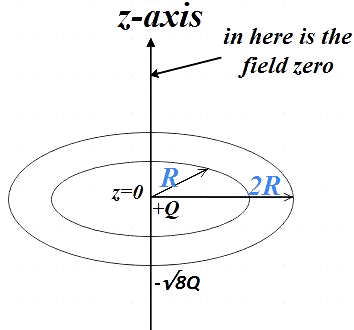
Two concentric rings, one of radius R and total charge +Q and the second of radius 2R and total charge $-\sqrt{8}Q$ lie in the x-y plane (i.e., z=0 plane). The common centre of rings lies at origin and the common axis coincides with z-axis. The charge is uniformly distributed on both rings. At what distance from the origin in the net electric field on z axis zero.

Answer 1

Hint: Recall the expression for electric field due to a circular ring on its axis. Also, remember that the electric fields due to both rings are directed opposite to each other. You could now find the distance at which the sum of these fields is zero.

Formula used:
Expression for electric field due to a circular ring on its axis,
$E=\dfrac{kQx}{{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}}}$

Complete step by step answer:
In the question we are given two concentric rings with uniform charge distribution, one with $+Q$ and the other with $-\sqrt{8}Q$ and have radii R and 2R respectively. They both have their common centre at origin and their common axis is the z-axis. We are asked to find the distance of the point on the z-axis at which the sum of the electric field produced by both rings is zero.
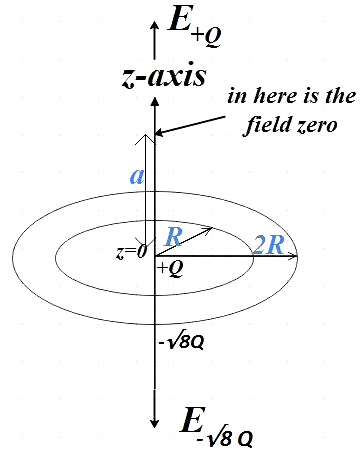
Since both rings have opposite charges, the electric field produced by them will be directed opposite to each other. So, if the electric field due to a ring with charge +Q was directed upwards the field due to others will be directed downward.

We know that, the electric field due to a charged ring along its axis is given by the formula,
$E=\dfrac{kQx}{{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}}}$
Where, Q is the uniform charge on the ring, R is the radius of the ring and x is the distance from the centre of the ring along its axis.
For ring with charge +Q and radius R, the electric field at the point at distance a from z=0 is,
${{E}_{1}}=\dfrac{kQa}{{{\left( {{a}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}}}$ ……………………………….. (1)
For ring with charge $-\sqrt{8}Q$ and radius 2R, the electric field at the point at distance a from z=0 is,
${{E}_{2}}=\dfrac{k\left( -\sqrt{8}Q \right)a}{{{\left( {{a}^{2}}+{{\left( 2R \right)}^{2}} \right)}^{\dfrac{3}{2}}}}$ …………………………………. (2)
At the point a, the net electric field is zero,
$\Rightarrow {{E}_{1}}+{{E}_{2}}=0$
$\Rightarrow \dfrac{kQa}{{{\left( {{a}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}}}=\dfrac{k\sqrt{8}Qa}{{{\left( {{a}^{2}}+{{\left( 2R \right)}^{2}} \right)}^{\dfrac{3}{2}}}}$
$\Rightarrow {{\left( {{a}^{2}}+4{{R}^{2}} \right)}^{\dfrac{3}{2}}}=\sqrt{8}{{\left( {{a}^{2}}+{{R}^{2}} \right)}^{\dfrac{3}{2}}}$
$\Rightarrow {{a}^{2}}+4{{R}^{2}}=2\left( {{a}^{2}}+{{R}^{2}} \right)$
$\Rightarrow {{a}^{2}}=2{{R}^{2}}$
$\therefore a=\sqrt{2}R$

Therefore, at a point at distance $a=\sqrt{2}R$ on the z-axis, the net electric field due to both rings is zero.

Note:
In questions like this, it is better that you memorize the standard expression for the electric field. Doing so, will save you plenty of time. Also, if instead of the charge if the charge density of the ring was given, we have the relation,
$\lambda =\dfrac{Q}{2\pi R}$
Where, ‘$\lambda $’ is the charge density.