Question

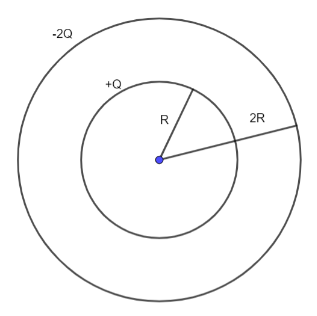
Two concentric conducting spheres of radii $R$ and $2R$ are carrying charges $Q$ and $2Q$ respectively. If the charge on the inner sphere is doubled, the potential difference between the spheres will

A. Become two times
B. Become four times
C. Be halved
D. Remains the same

Answer 1

Hint: In this question, we shall use the concept of potential difference between two concentric spheres which is given by $\Delta V = {V_A} - {V_B}$ where ${V_A}$ is the potential on the inner sphere while ${V_B}$ is the potential on the outer sphere. We shall calculate the respective potentials on every sphere for both the situations and then substitute in the above-mentioned formula. Then taking the ratio will give us our answer.

Formula used:
The potential difference between the two concentric spheres is given by,
$\Delta V = {V_A} - {V_B}$
where ${V_A}$ is the potential on the inner sphere while ${V_B}$ is the potential on the outer sphere.
Also, the potential on a sphere is calculated by,
$V = \dfrac{{kq}}{r}$
where $k$ is a constant equal to $\dfrac{1}{{4\pi {\varepsilon _0}}}$, $q$ is the charge on the sphere and $r$ is the distance from the center of the sphere where the charge is located.

Complete step by step answer:
The potential difference between the two concentric spheres is given by,
$\Delta V = {V_A} - {V_B}$
Initially when the charges were +Q and -2Q,
For the inner sphere,
${V_A} = \dfrac{{kQ}}{R} - \dfrac{{k(2Q)}}{{2R}}$
$ \Rightarrow {V_A} = 0$
For the outer sphere,
${V_B} = \dfrac{{kQ}}{{2R}} - \dfrac{{k(2Q)}}{{2R}}$
$ \Rightarrow {V_B} = \dfrac{{ - kQ}}{{2R}}$
So, the potential difference becomes $\Delta {V_i} = 0 - ( - \dfrac{{kQ}}{{2R}})$
$ \Rightarrow \Delta {V_i} = \dfrac{{kQ}}{{2R}}$

Now when the charge on the inner sphere is doubled,
For the inner sphere,
${V_A} = \dfrac{{k2Q}}{R} - \dfrac{{k(2Q)}}{{2R}}$
$ \Rightarrow {V_A} = \dfrac{{kQ}}{R}$
For the outer sphere,
${V_B} = \dfrac{{k2Q}}{{2R}} - \dfrac{{k(2Q)}}{{2R}}$
$ \Rightarrow {V_B} = 0$
So, the potential difference becomes $\Delta {V_f} = 0 - ( - \dfrac{{kQ}}{{2R}})$
$ \Rightarrow \Delta {V_f} = \dfrac{{kQ}}{R}$
Taking the ratio we get,
$\therefore \dfrac{{\Delta {V_f}}}{{\Delta {V_i}}} = \dfrac{2}{1}$

Hence, option A is the correct answer.

Note:We need to take good care of the sign convention while calculating the potential since any negligence in the sign could give wrong answers. Also, r is not the radius of the spheres rather the distance from the center of the sphere where the charge is located. But since the charge was present on the surface of the sphere, this distance became equal to the radius of the sphere.