Question

Two compound microscopes A and B were compared. Both had objectives and eyepieces with the same magnification but A gave an overall magnification that is greater than that of B. Which of the following is a possible explanation?
(A). The distance between the objective and eyepiece in A is greater than the corresponding distance in B.
(B). The distance between the objective and eyepiece in A is less than the corresponding distance in B.
(C). The eyepiece and objectives were reversed in A
(D). The eyepiece and objectives were reversed in B

Answer 1

Hint: A compound microscope has two lenses; objective lens and eye-piece. The size of the eye-piece is greater. The magnification depends on the magnification from both lenses and the final image is formed at least distance of distinct vision. Comparing the parameters used in overall magnification of compound microscopes A and B, we can determine the reason responsible for greater over magnification of A.

Formulas used:
$m=\dfrac{{{v}_{0}}}{{{u}_{0}}}\left( 1+\dfrac{{{f}_{e}}}{D} \right)$

Complete step-by-step solution:

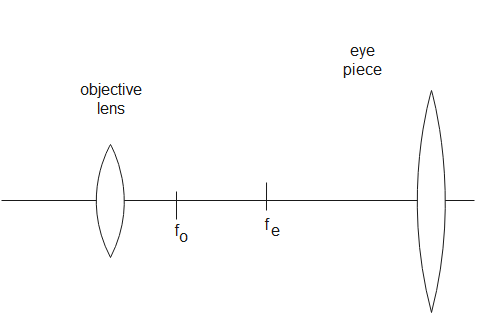
A microscope is used to see objects or organisms which are not visible to the naked eye. The purpose of a microscope is to magnify very small objects.

The formula for magnification by a compound microscope is given by-
When the final image is formed at $D$
$m=\dfrac{{{v}_{0}}}{{{u}_{0}}}\left( 1+\dfrac{{{f}_{e}}}{D} \right)$
Here,
$m$ is the magnification of the compound microscope
${{v}_{0}}$ is the image distance for the objective lens
${{u}_{0}}$ is the object distance for the objective lens
${{f}_{e}}$ is the focal length of eye-piece
$D$ is the least distance of distinct vision and its value is $25cm$.

The magnification of objectives and eye pieces of both microscopes is equal. Therefore,
$\dfrac{{{v}_{0}}}{{{u}_{0}}}=\dfrac{v{{'}_{0}}}{u{{'}_{0}}}$
Here,
${{v}_{0}}$ and ${{u}_{0}}$ are object and image distance for objective lens of microscope A
$v{{'}_{0}}$ and $u{{'}_{0}}$ are the object and image distances for the objective lens of microscope B.

Similarly,
$\dfrac{{{v}_{e}}}{{{u}_{e}}}=\dfrac{v{{'}_{e}}}{u{{'}_{e}}}$
Here,
${{v}_{e}}$ and ${{u}_{e}}$ are object and image distance for eye-piece of microscope A
$v{{'}_{e}}$ and $u{{'}_{e}}$ are the object and image distances for eye-piece of microscope B.

In compound microscopes the lenses are kept at a distance which depends on the sum of their focal lengths.
$L={{f}_{o}}+{{f}_{e}}$
Here,
$L$ is the distance between the lenses
${{f}_{o}}$ is the focal length of the objective
${{f}_{e}}$ is the focal length of the eye-piece

If the focal length of any of the lenses is increased, the distance between the lenses also increases.
Therefore, using eq (1), we can say that
$m=\dfrac{{{v}_{0}}}{{{u}_{0}}}\left( 1+\dfrac{{{f}_{e}}}{D} \right)$

The focal length of the eyepiece in microscope A is greater than in microscope B due to which the distance between the lenses in A increases than in B.

Therefore, the overall magnification of A is greater because the focal length of its eye-piece is greater which also increases the distance between the lenses.

Hence, the correct option is (A).

Note:
A simple microscope consists of only one lens while a compound microscope consists of two lenses. The final image formed in a microscope is virtual, inverted and enlarged. The focal length of the eye-piece must be greater than the objective to get greater magnification.