Question

Two coherent monochromatic point sources ${{S}_{1}}$ and ${{S}_{2}}$ of wavelength $\lambda =600\,\,nm$ are placed symmetrically on either side of the center of the circle as shown. The sources are separated by a distance $d=1.8\,\,mm$. This arrangement produces interference fringes visible as alternate bright and dark spots on the circumference of the circle. The angular separation between two consecutive bright spots is $\Delta \theta $. Which of the following options are correct?

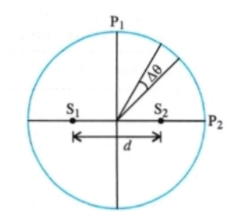
(A) The total number of fringes produced between ${{P}_{1}}$ and ${{P}_{2}}$ in the first quadrant is close to $3000$
(B) A dark spot will be formed at the point ${{P}_{2}}$
(C) At ${{P}_{2}}$ the order of fringe will be maximum
(D) The angular separation between two consecutive bright spots decreases as we move from ${{P}_{1}}$ to ${{P}_{2}}$ along the first quadrant

Answer 1

Hint: The interference taking place at points of maximum intensity is called constructive interference. For constructive interference phase difference should be zero or even multiple of $\pi $.
i.e. $\phi =2n\pi $, where $n=0,1,2,3,...$
Phase difference $\Delta x=n\lambda $
The interference taking place at points of minimum intensity is called destructive interference. For destructive interference phase difference should be an odd multiple of $\pi $
i.e. $\phi =(2n+1)\pi $, where $n=0,1,2,3,...$
Phase difference $\Delta x=(2n+1)\dfrac{\lambda }{2}$

Step by step solution:
Given: wavelength $\lambda =600\,\,nm$, separation between two source $d=1.8\,\,mm$
The path difference between the waves from ${{S}_{1}}$ and ${{S}_{2}}$ at the point ${{P}_{2}}$ is $d$.
∴ Number of fringes between ${{P}_{1}}$ and ${{P}_{2}}$,
$n=\dfrac{d}{\lambda }$
⇒ $n=\dfrac{1.8\times {{10}^{-2}}}{6\times {{10}^{-7}}}=3000$

Therefore, option (A) is correct.
As at ${{P}_{2}}$, ${{3000}^{th}}$ bright fringe is formed, i.e. order of fringe is maximum.
Therefore, option (C) is correct and option (B) is incorrect.
Angular separation between two consecutive maxima is given by,
$\dfrac{d\theta }{d\lambda }=\dfrac{\lambda }{d\cos \theta }$
As we move from ${{P}_{1}}\,$ to ${{P}_{2}}$ in first quadrant $\theta $ increases from ${{0}^{\circ }}$ to ${{90}^{\circ }}$, $\cos \theta $ decrease from $1$ to $0$, hence the angular separation between consecutive maxima increases.
Therefore, option (D) is incorrect.

Note: For bright fringes (maximum intensity) phase difference between two sources is $\lambda ,2\lambda ,3\lambda ,4\lambda \lambda ,5\lambda , ...$
Thus, waves should meet in the same phase or their crests should meet crests and troughs should meet troughs.
For dark fringe (minimum intensity) phase difference between two sources is \[\dfrac{\lambda }{2},\dfrac{3\lambda }{2},\dfrac{5\lambda }{2},\dfrac{7\lambda }{2},...\]
Thus, waves should meet in opposite phases or crests of one wave should meet troughs of another.