Question

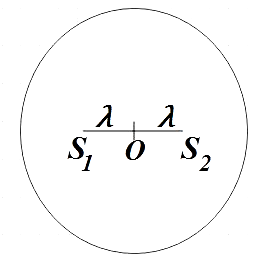
Two coherent light sources ${{S}_{1}}$ and ${{S}_{2}}$ are kept at equal distances $\lambda $ from the centre of circle on the same plane of the circle as shown in figure. In one complete revolution on the circular path, number of maxima observed is ($\lambda $= wavelength of light used)

A. 4
B. 6
C. 8
D. 12

Answer 1

Hint: To begin with you could consider an arbitrary point on the circular path and then find the path difference of the given two sources on that particular point. Now, you could recall the condition for constructive interference and hence get an expression for angular position for maxima in the given circular path. Now find all possible angular positions satisfying the above condition.

Formula used: Condition for constructive interference,
$\Delta x=n\lambda $

Complete step by step answer:
In the question, we are given two coherent light sources which are equidistant from the centre of a circle as shown in the figure. We are asked to find the number of maxima observed after one complete revolution of this circular path.

Let P be some point on the circular path and from the figure above, we see that the distance travelled by the light from source ${{S}_{1}}$ to reach the point P is ${{S}_{1}}P$ and the distance travelled by the light from source ${{S}_{2}}$ to reach the point P is${{S}_{2}}P$. Also, the path difference $\Delta x$ that is the difference in path taken by light to reach P from these two sources is,
$\Delta x={{S}_{1}}Q=\left( {{S}_{1}}P-{{S}_{2}}P \right)$
But,
$\cos \theta =\dfrac{\Delta x}{2\lambda }$
$\Rightarrow \Delta x=2\lambda \cos \theta $ …………………………. (1)
We are asked to find the number of maxima. The maxima is the point where constructive interference takes place for two coherent sources and the condition for constructive interference is that the path difference should be integral multiples of the wavelength. That is,
$\Delta x=n\lambda $ ………………………….. (2)
Where, n is an integer.
Equating (1) and (2),
$\Rightarrow 2\lambda \cos \theta =n\lambda $
$\Rightarrow \cos \theta =\dfrac{n}{2}$
$\Rightarrow \theta ={{\cos }^{-1}}\left( \dfrac{n}{2} \right)$ ………………………… (3)
We know that value of $\cos \theta $ varies from -1 to +1,
$\Rightarrow -1\le \cos \theta \le +1$
$\Rightarrow -1\le \dfrac{n}{2}\le +1$
$\Rightarrow -2\le n\le +2$
Therefore,
$n=0,\pm 1,\pm 2$
For each value of n let us find the angular position $\theta $ from (3).
For $n=0$
$\theta ={{\cos }^{-1}}\left( 0 \right)$
$\theta =90{}^\circ ,270{}^\circ $ ………………………….. (4)
For $n=\pm 1$
$\theta ={{\cos }^{-1}}\left( \dfrac{\pm 1}{2} \right)$
$\theta =60{}^\circ ,120{}^\circ ,240{}^\circ ,300{}^\circ $ ……………………….. (5)
For $n=\pm 2$
$\theta ={{\cos }^{-1}}\left( \pm \dfrac{2}{2} \right)={{\cos }^{-1}}\left( \pm 1 \right)$
$\theta =0{}^\circ ,180{}^\circ $ …………………………. (6)
Therefore, we have found a total of 8 maxima in the given circular path, they are,
$0{}^\circ ,60{}^\circ ,90{}^\circ ,120{}^\circ ,180{}^\circ ,240{}^\circ ,270{}^\circ ,300{}^\circ $
Hence, in one complete revolution on the circular path, the number of maxima that can be observed are 8.

So, the correct answer is “Option C”.

Note: You should remember that the term n in the condition for constructive interference is an integer. So n cannot be a fraction or anything else but integer. We see that $\theta =360{}^\circ $ is also a possible angular position for maxima but that is the same as $0{}^\circ $, so we shouldn’t consider that angular position.