Question

Two circles of radii $ 8 $ and $ 4 $ touch each other externally at a point A. A point B is taken on the larger circle through which a straight line is drawn touching the smaller circle at C. If $ AB = \sqrt 6 $ then find BC.

Answer 1

Hint: A shape that is round in figure, closed, two-dimensional and has no corners is termed as a circle. The midpoint of the circle is called the centre of the circle. A line segment that connects the centre of the circle to the point that is on the circle itself is termed as radius. The line which touches the circle at only one point is called the tangent of the circle.
Formula Used: Length of common tangent $ = \sqrt {{d^2} - {{\left( {{r_1} - {r_2}} \right)}^2}} $
Where d is the distance between two circles, $ {r_1},{r_2} $ are the radius of the circles.

Complete step-by-step answer:
Let us draw a rough figure of circles, one is bigger and the other one is smaller with center O of bigger circle whose radius is $ 8 $ and with centre P of smaller circle whose radius is $ 4 $ . Now, we will follow the instructions as given in the question above,

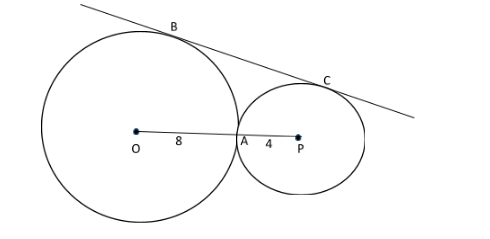
The line BC formed is the common tangent of both the circles and we have to find the length of line BC.
Distance between two circles (d) is $ 8 + 4 = 12 $ , radius of the bigger circle $ \left( {{r_1}} \right) $ is $ 8 $ and radius of the smaller circle $ \left( {{r_2}} \right) $ is $ 4 $ , now substitute the values in the above formula,
 $
  BC = \sqrt {{{12}^2} - {{\left( {8 - 4} \right)}^2}} \\
  BC = \sqrt {144 - {4^2}} \\
  BC = \sqrt {144 - 16} \\
  BC = \sqrt {128} \\
  BC = 8\sqrt 2 \;
  $
Hence, the value of BC is $ 8\sqrt 2 $ .
So, the correct answer is “$ 8\sqrt 2 $”.

Note: There is a direct formula to find the length of common tangent i.e, $ \sqrt {{r_1}{r_2}} $ , where $ {r_1} $ is the radius of the larger circle i.e, $ 8 $ and $ {r_2} $ is the radius of the smaller circle i.e, $ 4 $ . Now, we will find the length of BC by substituting the values into the given formula, we get,
 $
  BC = \sqrt {{r_1}{r_2}} \\
  BC = \sqrt {8 \times 4} \\
  BC = \sqrt {32} \\
  BC = 8\sqrt 2 \;
  $