Question

Two chords of lengths \[30\,{\text{cm}}\] and \[16\,{\text{cm}}\] are on the opposite side of the centre of the circle. If the radius of the circle is \[17\,{\text{cm}}\] , find the distance between the two chords.

Answer 1

Hint: To find the distance between the two chords we need to find the perpendicular distance between them, which is the shortest distance. A perpendicular drawn from the centre to a chord, bisects the chord. We will apply Pythagora's theorem and manipulate accordingly to find the desired result.

Complete step-by-step answer:
In the given question, we are supplied with the following data;

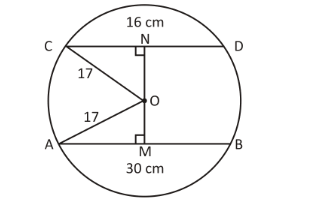
There is a circle whose radius is \[17\,{\text{cm}}\] .
There are two chords of lengths \[30\,{\text{cm}}\] and \[16\,{\text{cm}}\] are on the opposite side of the centre of the circle.
We are asked to find the distance between the two chords.
To begin with, first of all, we need to draw the diagram for better understanding.
In the diagram we will join \[OA\] and \[OC\] .
We draw \[ON\] perpendicular to \[CD\] and \[OM\] perpendicular to \[AB\] .
We know, a perpendicular drawn from the centre to a chord, bisects the chord.
So, we will find the length of \[CN\] and \[AM\] .
$
CN = \dfrac{1}{2} \times CD \\
\Rightarrow CN = \dfrac{1}{2} \times 16 \\
\Rightarrow CN = 8\,{\text{cm}} \\
AM = \dfrac{1}{2} \times AB \\
\Rightarrow AM = \dfrac{1}{2} \times 30 \\
\Rightarrow AM = 15\,{\text{cm}}
$
In the triangle \[OCN\] , we apply Pythagoras theorem:
$
O{C^2} = O{N^2} + C{N^2} \\
\Rightarrow {17^2} = O{N^2} + {8^2} \\
\Rightarrow O{N^2} = {17^2} - {8^2} \\
\Rightarrow O{N^2} = 225
$
 \[ \Rightarrow ON = 15\,{\text{cm}}\]

Again, in the triangle \[{\text{OAM}}\] , we apply Pythagoras theorem:
$
O{A^2} = O{M^2} + A{M^2} \\
\Rightarrow {17^2} = O{M^2} + {15^2} \\
\Rightarrow O{M^2} = {17^2} - {15^2} \\
\Rightarrow O{N^2} = 64
$
 \[ \Rightarrow ON = 8\,{\text{cm}}\]
So, we have found out the length of the two perpendiculars.
Now, we can find the distance between the two chords by adding the two perpendicular distances.
$ NM = ON + OM \\
\Rightarrow NM = 15 + 8 \\
\Rightarrow NM = 23\,{\text{cm}} \;
$
Hence, the distance between the two chords is \[23\,{\text{cm}}\] .
So, the correct answer is “ \[23\,{\text{cm}}\] ”.

Note: While solving the problem, it is important to remember that a perpendicular drawn from a centre to the chord always bisects the chord. Conversely, we can also say that, if we join the midpoint of the chord and the centre, the line is always the perpendicular. It is important to note that in a right-angled triangle, the largest side is the hypotenuse.