Question

Two charges $q$ and $-3q$ are fixed on the x-axis separated by a distance $d$. Where should a third charge $2q$ be placed from $A$ such that it will not experience any force?
 

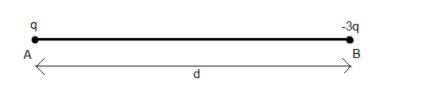
$A)\text{ }\dfrac{\sqrt{3}d-d}{2}$
$B)\text{ }\dfrac{d+\sqrt{3}d}{2}$
$C)\text{ }\dfrac{3d}{2}$
$D)\text{ }\dfrac{5d}{2}$

Answer 1

Hint: This problem can be solved by using Coulomb’s law for the force on the charge due to the other two charges. Unlike charges attract each other whereas like charges repel each other. Therefore, the positive charge $q$ will exert a repulsive force on the charge $2q$ and the charge $-3q$ will exert an attractive force.

Formula used:
$F=K\dfrac{Qq}{{{r}^{2}}}$

Complete step-by-step answer:
Since like charges attract repel each other while unlike charges attract each other, students must realize that if the third charge is placed in between the two charges, the repulsive force due to the positive charge and the attractive force due to the negative charge will be in the same direction and therefore, the charge will not be in equilibrium.
Therefore, we will place the charge at a distance $x$ from the charge $q$ in a direction away from the charge $-3q$ as shown below.

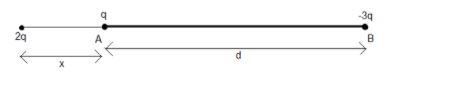
Now, the Coulomb force $F$ on a charge $q$ due to another charge $Q$ placed at a distance $r$ from it is given by
$F=K\dfrac{Qq}{{{r}^{2}}}$ --(1)
Where $K=9\times {{10}^{9}}kg.{{m}^{3}}{{s}^{-2}}{{C}^{-2}}$
Now, using (1), we get the sum of the forces on the charge $2q$ due to the charges $q$ and $-3q$ as
$F=K\dfrac{q\left( 2q \right)}{{{x}^{2}}}+K\dfrac{-3q\left( 2q \right)}{{{\left( d+x \right)}^{2}}}=2K{{q}^{2}}\left[ \dfrac{1}{{{x}^{2}}}-\dfrac{3}{{{\left( d+x \right)}^{2}}} \right]$
Now, for equilibrium, $F=0$
$\Rightarrow 2K{{q}^{2}}\left[ \dfrac{1}{{{x}^{2}}}-\dfrac{3}{{{\left( d+x \right)}^{2}}} \right]=0$
$\Rightarrow \left[ \dfrac{1}{{{x}^{2}}}-\dfrac{3}{{{\left( d+x \right)}^{2}}} \right]=0$
$\Rightarrow \dfrac{1}{{{x}^{2}}}=\dfrac{3}{{{\left( d+x \right)}^{2}}}$
$\Rightarrow {{\left( d+x \right)}^{2}}=3{{x}^{2}}$
Square rooting both sides we get
$\Rightarrow \sqrt{{{\left( d+x \right)}^{2}}}=\sqrt{3{{x}^{2}}}$
$\Rightarrow d+x=\sqrt{3}x$
$\Rightarrow \sqrt{3}x-x=d$
$\Rightarrow x\left( \sqrt{3}-1 \right)=d$
$\Rightarrow x=\dfrac{d}{\sqrt{3}-1}$
Rationalizing, we get
$x=\dfrac{d\left( \sqrt{3}+1 \right)}{\left( \sqrt{3}-1 \right)\left( \sqrt{3}+1 \right)}=\dfrac{d\left( \sqrt{3}+1 \right)}{{{\sqrt{3}}^{2}}-{{1}^{2}}}=\dfrac{d\left( \sqrt{3}+1 \right)}{3-1}=\dfrac{d+\sqrt{3}d}{2}$ $\left( \because \left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}} \right)$
Therefore, we have got the required expression for the distance from $A$ that the third charge has to be kept.
Therefore, the correct option is $B)\text{ }\dfrac{d+\sqrt{3}d}{2}$.

So, the correct answer is “Option B”.

Note: While putting the square root in the calculation, we neglected the negative root since doing that would mean that $d$ would turn out to be negative which is not possible as $d$ is the measure of a distance and it has to be positive. Students must realize that if they put the charge in between the two charges, it will never be in equilibrium upon seeing the question and hence, must not waste time by placing the charge in between the two charges and waste time in calculating an impossible answer.