Question

Two charges, each equal to$\;q$, are kept at $x=-a$ and $x=a$ on the x-axis. A particle of mass$\;m$ and charge $q_0 = \dfrac{q}{2}$ is placed at the origin. If charge $q_0$ is given a small displacement $\left( y<< a \right)$ along the y-axis, the net force acting on the particle is proportional to:
A). $\;-y$
B). $\dfrac{1}{y^2}$
C). $-\dfrac{1}{y}$
D). $\;y$

Answer 1

Hint: Recall that since the charges and the particle possess like charges, they experience a repulsive force. This repulsive force is directed from the charges towards the particle since the particle possesses a lesser electric charge than the charges themselves. Resolve this force exerted by each charge into horizontal and vertical components and determine the resultant force acting in both the directions. To this end, additively find the net force acting on the particle and arrive at an appropriate expression that establishes a relationship between the net force and the particle displacement.
Formula Used:
Coulomb’s Law: $F = \dfrac{kq_1q_2}{r^2}$

Complete step-by-step solution:
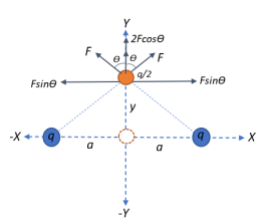
We are given that two charges, each having a charge$\;q$ are kept opposite to each other along the x-axis at a distance of$\;a$ from the origin. Another particle of charge $\dfrac{q}{2}$ is placed along the y-axis at a distance$\;y$ from the origin as shown in the figure. The charges$\;q$ each exert a repulsive force directing outwards on the particle as shown.
Let the magnitude of force exerted by each charge$\;q$ on the particle of charge $\dfrac{q}{2}$ be$\;F$. From Coulomb’s law, this will be equivalent to:
$F = \dfrac{kq\left(\dfrac{q}{2}\right)}{r^2}$
where k is the Coulomb’s constant, and r is the distance between the charges$\;q$ and $\dfrac{q}{2}$
The distance between$\;q$ and $\dfrac{q}{2}$ can be found by applying Pythagora's theorem to one of the right angles formed, as shown in the figure.
$\Rightarrow r^2 = y^2+a^2 \Rightarrow r =\sqrt{y^2+a^2}$

Therefore, $F = \dfrac{kq^2}{2\left(y^2+a^2\right)}$
To find the net force acting on the particle, we resolve the force that they exert on the particle into their respective horizontal and vertical components. Let $\theta$ be the angle that the force exerted by the charges makes with the y-axis.
The net force along the horizontal direction will be:
 $F_{H} = F\;sin\theta + (-F\;sin\theta) = F\;sin\theta – F\;sin\theta = 0$
Therefore, no force acts on the particle of charge $\dfrac{q}{2}$ in the horizontal direction.
The net force acting along the vertical direction will be:
$F_{V} = F\;cos\theta + F\;cos\theta = 2F\;cos\theta$
Therefore, the total force acting on the particle of charge $\dfrac{q}{2}$ will be the sum of the forces acting on it in the horizontal and vertical directions, i.e.,
$F_{net} = F_{H} +F_{V} = 0 + 2F\;cos\theta = 2F\;cos\theta$
But $F = \dfrac{kq^2}{2\left(y^2+a^2\right)}$
Therefore, $F_{net} = \dfrac{2kq^2}{2\left(y^2+a^2\right)}\;cos\theta = \dfrac{kq^2}{\left(y^2+a^2\right)}\;cos\theta$
From the diagram, taking any one of the right-angled triangles, we have:
$cos\theta = \dfrac{y}{r} = \dfrac{y}{\sqrt{\left(y^2+a^2\right)}}$
Plugging this into our net force equation we get:
$F_{net} = \dfrac{2kq^2}{2\left(y^2+a^2\right)}\;cos\theta = \dfrac{kq^2}{\left(y^2+a^2\right)}. \dfrac{y}{\sqrt{\left(y^2+a^2\right)}}$
$\Rightarrow F_{net} = \dfrac{kq^2y}{\left(y^2+a^2\right)^{3/2}}$
But we are given that $y << a$ which means that we can approximate $y^2 +a^2 \approx a^2$, so the above equation becomes:
$F_{net} = \dfrac{kq^2y}{\left(a^2\right)^{3/2}} = \dfrac{kq^2y}{\left(a^2\right)}$
$\Rightarrow F_{net} \propto y$
Therefore, the correct option is D.$\;y$

Note: While resolving the vectors into their horizontal and vertical components, remember to assign the sine and cosine values correctly since it is a common misconception that the horizontal side is always the cosine part and the vertical side is the sine part.
The correct way to go about this would be to establish that the component that is adjacent to $\theta$ assumes a cosine value, whereas the component that is opposite to $\theta$ assumes a sine value.