Question

Two charges $ 5\mu C $ and $ - 3\mu C $ are located $ 16cm $ apart. At what points on the line joining the two charges is the electric potential zero?

Answer 1

Hint: First draw a rough diagram as per the given statement. Then assume a point on the line joining the two charges and let the point mark as x cm away from $ 5\mu C $ charge. Then write the total potential at that assumed point and equate it with zero as the electric potential at that point is zero. On further solving we can find the value of x which is our required answer.

Complete answer:
Electric potential:
It is defined as the amount of work energy needed to move a unit electric change from one point to another specific point in an electric field.
Formula of the electric potential:
 $ V = \dfrac{1}{{4\pi \varepsilon 0}} \times \dfrac{q}{d} $
Where,
V is the electric potential of the charge.
 $ \dfrac{1}{{4\pi \varepsilon 0}} $ is a constant term which we can replace with k.
The charge is equal to q.
The distance at which we are calculating the electric potential of the charge is d.
As per the given problem we have two charges $ 5\mu C $ and $ - 3\mu C $ are located $ 16cm $ apart. Now we need to calculate the point on the line joining the two charges where the net electric potential due to these point charges is zero.
Let us assume a point which is x distance from the change $ 5\mu C $ on the line where the net electric potential is zero.

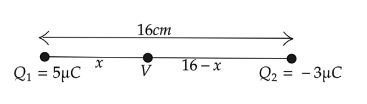
The electric potential at point x due to $ 5\mu C $ is,
 $ V5 = \dfrac{{kq5}}{x} $
Now putting the known value we will get,
 $ V5 = \dfrac{{k\left( {5\mu C} \right)}}{x} \ldots \ldots \left( 1 \right) $
If the distance is x from cgnafe $ 5\mu C $ the for change $ - 3\mu C $ the distance will be $ 16 - x $ as the toa distance between the two p[pint is $ 16cm $
The electric potential at point $ 16 - x $ due to $ - 3\mu C $ is,
 $ V - 3 = \dfrac{{kq - 3}}{{16 - x}} $
Now putting the known value we will get,
 $ V - 3 = \dfrac{{k\left( { - 3\mu C} \right)}}{{16 - x}} \ldots \ldots \left( 2 \right) $
Now the net electric potential at that point be,
 $ V = V5 + V - 3 $
Putting equation $ \left( 1 \right) $ and $ \left( 2 \right) $ we will get,
 $ V = \dfrac{{k\left( {5\mu C} \right)}}{x} + \dfrac{{k\left( { - 3\mu C} \right)}}{{16 - x}} $
 $ \Rightarrow V = \dfrac{{k\left( {5\mu C} \right)}}{x} - \dfrac{{k\left( {3\mu C} \right)}}{{16 - x}} $
As per the problem the electric potential at that point is zero.
Now,
 $ 0 = \dfrac{{k\left( {5\mu C} \right)}}{x} - \dfrac{{k\left( {3\mu C} \right)}}{{16 - x}} $
 $ \Rightarrow \dfrac{{k\left( {5\mu C} \right)}}{x} = \dfrac{{k\left( {3\mu C} \right)}}{{16 - x}} $
Cancelling the common term we will get,
 $ \dfrac{5}{x} = \dfrac{3}{{16 - x}} $
Rearranging the term we will get,
 $ 5\left( {16 - x} \right) = 3x $
 $ \Rightarrow 80 - 5x = 3x $
 $ \Rightarrow 80 = 3x + 5x \Rightarrow x = \dfrac{{80}}{8} = 10cm $
Hence the point from the $ - 3\mu C $ will be $ \left( {16 - x} \right) = 16 - 10 = 6cm $ .

Note:
Here in the above problem we assume the given point x inside the line joins two charges. If we assume that point outside of the line joining two points. Where the net potential will be zero.

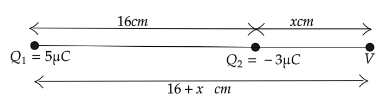
 $ V5 = \dfrac{{k\left( {5\mu C} \right)}}{{\left( {16 + x} \right)}} \ldots \ldots \left( 1 \right) $
 $ V - 3 = \dfrac{{k\left( { - 3\mu C} \right)}}{x} \ldots \ldots \left( 2 \right) $
Net electric potential be,
 $ V = V5 + V - 3 $
Putting values,
 $ V = \dfrac{{k\left( {5\mu C} \right)}}{{\left( {16 + x} \right)}} + \dfrac{{k\left( { - 3\mu C} \right)}}{x} = \dfrac{{k\left( {5\mu C} \right)}}{{\left( {16 + x} \right)}} - \dfrac{{k\left( {3\mu C} \right)}}{x} $
Equatind net electric potential to zero,
 $ 0 = \dfrac{{k\left( {5\mu C} \right)}}{{\left( {16 + x} \right)}} - \dfrac{{k\left( {3\mu C} \right)}}{x} $
 $ \Rightarrow \dfrac{{k\left( {5\mu C} \right)}}{{\left( {16 + x} \right)}} = \dfrac{{k\left( {3\mu C} \right)}}{x} $
Canceling the common terms we will get,
 $ \dfrac{{\left( 5 \right)}}{{\left( {16 + x} \right)}} = \dfrac{{\left( 3 \right)}}{x} $
Rearranging,
 $ 5x = 3\left( {16 + x} \right) $
On solving we will get,
 $ x = 12cm $ which is the distance from $ - 3\mu C $ change.
Hence the distance from the $ 5\mu C $ charge be $ 16 + x = 16 + 12 = 40cm $ .