Question

Two charges $4\times {{10}^{-9}}C$ and $-16\times {{10}^{-9}}C$ are separated by a distance 20 cm in air. The position of the neutral point from the small charge is:
$\left( A \right)\dfrac{40}{3}cm$
$\left( B \right)\dfrac{20}{3}cm$
$\left( C \right)40cm$
$\left( D \right)\dfrac{10}{3}cm$
$\left( E \right)20cm$

Answer 1

Hint: In order to find the neutral point from the small charge, we will use Coulomb’s law. This is because by the use of this formula we will be able to find the required distance of the neutral point without hindering the positions of the charges.
Formula used: $F=k\dfrac{\left| \left. {{q}_{1}}{{q}_{2}} \right| \right.}{{{r}^{2}}}$ where, ${{q}_{1}},{{q}_{2}}$ are the respective charges which are separated by a distance if r units and$k=\dfrac{1}{4\pi {{\in }_{\text{o}}}}$.

Complete step by step answer:
Electric charge: It is a basic property of any kind of matter that is present around us. It carries some particles that are elementary. These charges are of two types namely, a positive charge and a negative charge. These charges can neither be created nor destroyed by anything. Instead of this, the charges can only be transferred from one object to another object.
Electric field: By this term we mean the electric force that is present around the field. In that field, the electric force on a unit charge shows its intensity. The SI unit of the electric field is normally Newton per coulomb.
Coulomb’s Law: By coulomb’s law we mean the magnitude of the force, in the form of electricity, between any two charges which are directly proportional to the magnitude of the product of the two charges and also, inversely proportional to the square of the distance between them.
In the question, we are given that there is a presence of a neutral electric charge between the two charges. Since the two charges have unlike charges on them, this neutral charge will lie on the outside of the line which joins these two charges. Suppose that charge $4\times {{10}^{-9}}C$ is A and the charge $-16\times {{10}^{-9}}C$ is B. Consider that the charge C be the neutral point as a small one. The diagram showing this is given below.

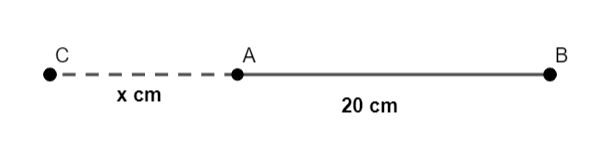
The neutral point should be placed nearer to the charge with a smaller magnitude than the other charge. Since the magnitude of B charge is greater, the neutral point will be placed nearer to charge A. We are taking the charge of C as Q. Now, we are given AB = 20cm and we need to find AC = x cm.
So, by using the formula $F=k\dfrac{\left| \left. {{q}_{1}}{{q}_{2}} \right| \right.}{{{r}^{2}}}$ we will have \[{{\overrightarrow{F}}_{CA}}=\dfrac{1}{4\pi {{\in }_{\text{o}}}}\times \dfrac{\left| \left. \left( 4\times {{10}^{-9}}C \right)\left( Q \right) \right| \right.}{{{\left( x \right)}^{2}}}\] and \[{{\overrightarrow{F}}_{CB}}=-\dfrac{1}{4\pi {{\in }_{\text{o}}}}\times \dfrac{\left| \left. \left( -16\times {{10}^{-9}}C \right)\left( Q \right) \right| \right.}{{{\left( 20+x \right)}^{2}}}\]
Now, the total net force on C by charges A and B will be
${{\overrightarrow{F}}_{C}}={{\overrightarrow{F}}_{CA}}+{{\overrightarrow{F}}_{CB}}$
$\Rightarrow {{\overrightarrow{F}}_{C}}=\dfrac{1}{4\pi {{\in }_{\text{o}}}}\times \dfrac{\left( 4\times {{10}^{-9}}C \right)\left( Q \right)}{{{x}^{2}}}-\dfrac{1}{4\pi {{\in }_{\text{o}}}}\times \dfrac{\left( 16\times {{10}^{-9}}C \right)\left( Q \right)}{{{\left( 20+x \right)}^{2}}}$
$\Rightarrow {{\overrightarrow{F}}_{C}}=\dfrac{Q}{4\pi {{\in }_{\text{o}}}}\times \left( \dfrac{\left( 4\times {{10}^{-9}}C \right)}{{{x}^{2}}}-\dfrac{\left( 16\times {{10}^{-9}}C \right)}{{{\left( 20+x \right)}^{2}}} \right)$
Due to the presence of the neutral charge we will have that the force on C will be 0. This means that $\left| \left. {{\overrightarrow{F}}_{C}} \right| \right.=0$ . This results into,
$\Rightarrow \left| \left. \dfrac{Q}{4\pi {{\in }_{\text{o}}}}\times \left( \dfrac{\left( 4\times {{10}^{-9}}C \right)}{{{x}^{2}}}-\dfrac{\left( 16\times {{10}^{-9}}C \right)}{{{\left( 20+x \right)}^{2}}} \right) \right| \right.=0$
$\Rightarrow \left| \left. \dfrac{\left( 4\times {{10}^{-9}}C \right)}{{{x}^{2}}}-\dfrac{\left( 16\times {{10}^{-9}}C \right)}{{{\left( 20+x \right)}^{2}}} \right| \right.=0$
$\Rightarrow \left| \left. \dfrac{4}{{{x}^{2}}}-\dfrac{16}{{{\left( 20+x \right)}^{2}}} \right| \right.=0$
$\Rightarrow \left| \left. \dfrac{4}{{{x}^{2}}} \right| \right.=\left| \left. \dfrac{16}{{{\left( 20+x \right)}^{2}}} \right| \right.$
$\Rightarrow \dfrac{{{\left( 20+x \right)}^{2}}}{{{x}^{2}}}=\dfrac{16}{4}$
If we take roots on both the sides of the equation so we get,
\[\Rightarrow \sqrt{\dfrac{{{\left( 20+x \right)}^{2}}}{{{x}^{2}}}}=\sqrt{\dfrac{16}{4}}\]
\[\Rightarrow \dfrac{20+x}{x}=\sqrt{4}\]
\[\Rightarrow \dfrac{20+x}{x}=\pm 2\]
\[\Rightarrow \dfrac{20+x}{x}=2\,\,or\,\,\Rightarrow \dfrac{20+x}{x}=-2\]
\[\Rightarrow 20+x=2x\,\,or\,\,20+x=-2x\]
\[\begin{align}
  & \Rightarrow 2x-x=20\,\,or\,\,2x+x=-20 \\
 & \Rightarrow x=20\,\,or\,\,3x=-20 \\
 & \Rightarrow x=20\,\,or\,\,x=-\dfrac{20}{3} \\
\end{align}\]
As distance cannot be negative so the value of x as $-\dfrac{20}{3}$ is rejected and x = 20 is accepted.
Hence, the correct option is (e) 20 cm.

Note:
We need to take the following things under consideration while solving the question:
(1) If there is no change of centimeters to meters then also the answer will be correct because we are already given the options in centimeters.
(2) As we are given two dislike charges, it is important that the neutral point will not lie between the charges but it will lie outside the line joining them.
(3) The presence of the neutral point should be nearer to the charge whose magnitude is less than the magnitude of the other.